Nota: R = conjunto dos números reais
|
Duas equações irracionais bastante interessantes: a segunda , muito mais que a primeira. |
1
- Resolva
a seguinte equação irracional em R:
Nota: R = conjunto dos números reais
![]()
Solução:
A
raiz quadrada no denominador do primeiro membro nos indica claramente
que x é um número real positivo, pois não existe
raiz quadrada real de número negativo e o denominador de uma
expressão não pode ser nulo, pois não existe
divisão por zero.
A equação
acima é dita irracional porque contém uma incógnita
sob radical, no caso o Öx
.
Posto isto, façamos Öx
= y , de onde tiramos x = y2 .
Substituindo na equação
dada fica:
50y2 / y = (y2 / 2) +
500
Simplificando, lembrando que y > 0, pois y = Öx
, vem:
50y = y2 / 2 + 500
Multiplicando
ambos os membros por 2, teremos:
100y
= y2 + 1000
Arrumando convenientemente,
vem:
y2 – 100y + 1000 = 0
Trata-se
de uma equação do segundo grau em y , do tipo ay2
+ by + c = 0, cuja
resolução pode ser feita pela aplicação da fórmula de
Bhaskara:
y = (-b ±
ÖD)
/ 2a onde D
= b2
– 4ac, termo conhecido como discriminante.
No nosso
caso temos: a = 1, b = -100 e c = 1000.
Aplicando a fórmula
acima teremos então:
y = (100 ±
20Ö15) / 2 = 50
± 10Ö15
Lembrando
que y > 0, observe que ambas raízes servem ao problema, já
que
tanto 50 + 10Ö15 como
50 - 10Ö15 são números
positivos.
Lembrando que x = y2 vem,
substituindo:
x = (50 ±
10Ö15)2 = 502
± 2.50.10Ö15
+ (10Ö15)2 = 4000 ±
1000Ö15
Portanto, as
raízes procuradas são:
x
= 4000 + 1000Ö15
ou x = 4000 - 1000Ö15
Portanto,
as raízes da equação dada são dois
números irracionais, cujos
valores aproximados são :
x1 = 4000 +
1000Ö15 = 1000(4 +
Ö15) @
7872,9833
x2 = 4000 - 1000Ö15
= 1000(4 -
Ö15) @ 127,0167
Por simples
substituição dos valores na equação
original, confirmamos que os valores acima são realmente as
soluções da equação proposta.
2
- Agora resolva esta equação irracional em R :
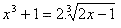
Veja a solução desta equação AQUI.
Paulo
Marques, 08 de agosto de 2002 – ampliado em 27/10/2008 - Feira de Santana – BA.
VOLTAR