| Num Centro Esportivo na UFBA em 1993 |
UFBA 1993) O diretor de um Centro Esportivo vai cercar um campo de forma
retangular e depois dividi-lo com outra cerca, para formar duas quadras
retangulares. A cerca que vai dividir o campo internamente custa Cr$ 10000,00
por metro, e a cerca externa custa
Cr$ 25000,00 por metro.
Sabendo-se que o diretor dispõe de Cr$ 4.800.000,00
para realizar a obra, determine o semiperímetro do campo de maior área cercada
possível.
Nota: UFBA = Universidade Federal da Bahia
Solução:
Nota: vemos que em 1993 a moeda oficial era o cruzeiro – Cr$ - que tinha uma
"porrada" de zeros.
Os Cr$ 4.800.000,00 daquela época, valeriam hoje cerca de R$1012,00. Não
calculei isto; usei um programinha de atualização monetária de um CD
que adquiri numa banca de revistas.
Veja a figura a seguir:
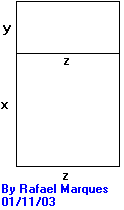
onde x, y e z são as medidas expressas em metros (m).
O perímetro (soma das medidas dos lados) do campo de forma retangular é igual
a:
P = x + y + z + x + y + z = 2(x + y + z)
O custo para construir esta cerca será então:
C1 = 2(x + y + z) . Cr$25000,00 = 50000(x + y + z)
A cerca que vai dividir o campo em duas quadras retangulares tem comprimento z.
Logo, o custo para construí-la será C2 = z . Cr$10000,00 = 10000z
O custo total será igual a C = C1 + C2 = 50000(x + y + z)
+ 10000z
Desenvolvendo a expressão acima, fica:
C = 50000x + 50000y + 50000z + 10000z = 50000x + 50000y + 60000z
Como o diretor dispõe de Cr$4.800.000,00 o custo total deverá ser igual a esse
valor, ou seja:
50000x + 50000y + 60000z = 4800000
Dividindo ambos os membros por 10000 , para eliminar os zeros, vem:
5x + 5y + 6z = 480 (equação 1)
A área do campo de forma retangular será igual a : S = (x + y) . z,
conforme pode-se inferir (deduzir ) da figura acima.
Da equação (1) acima, vem: 5(x + y) + 6z = 480
Daí tiramos x + y = (480 – 6z) / 5
Então, a área S será igual a S = [(480 – 6z) / 5] . z = [(480/5) –
(6z/5)].z
Desenvolvendo, fica:
S = (480z / 5) – (6z2 / 5)
Observe que a área S é uma função quadrática de z, ou seja,
S = (- 6/5) z2 + (480/5) z
Temos então uma função quadrática S = f(z) da forma
S = az2 + bz + c onde a = - 6/5, b = 480/5 e c = 0.
Como vocês estão acostumados com a função quadrática na forma y = ax2
+ bx + c, aqui é como se o S fosse o y e o z fosse o x. Porém, isto não muda
nada no problema.
Observe que na função S = (- 6/5) z2 + (480/5) z , temos que a <
0 e, portanto, a função possui um valor máximo, como já sabemos do estudo
das funções quadráticas
ou funções do segundo grau.
Como queremos determinar os valores de x, y e z (veja figura acima) para que a
área seja máxima, vamos começar determinando o valor de z para que S seja
máxima, ou seja, calcular o zv (coordenada do vértice) da função
S = (- 6/5) z2 + (480/5) z.
Teremos:
![]()
Ora, como z = 40, e x + y = (480 – 6z) / 5 conforme vimos acima, vem,
substituindo o valor de z:
x + y = (480 – 6.40) / 5 = (480 – 240) / 5 = 240 / 5 = 48
Portanto, como x + y = 48 e z = 40, o perímetro P que é a soma das medidas dos
lados será igual a
P = 2(x + y + z) = 2(48 + 40) = 176 metros = 176 m
Mas, o problema pede o semiperímetro, ou seja, a metade do perímetro. Logo, o
semiperímetro p será igual a
p = P/2 = 2(x + y + z) / 2 = 176/2 = 88 = 88 metros = 88 m , que é a resposta do problema.
Resposta: para que a área seja máxima, o semiperímetro do campo retangular
deverá ser igual a 88 m.
Agora resolva este:
Qual a área máxima do campo de forma retangular do exercício anterior?
DICA: Basta fazer z = 40 na função S = (- 6/5) z2 + (480/5) z , ou
calcular a ordenada do vértice através da conhecida fórmula Sv = yv
= - D / 4 a . Observe que usei a letra y
apenas porque vocês estão acostumados a escrever a função
quadrática como
y = ax2 + bx + c. Na verdade não seria necessário isto.
Resposta: área máxima = 1920 metros quadrados = 1920 m2
Paulo Marques,
08 de novembro de 2003 - Feira de Santana - BA
VOLTAR