Em um ciclo de três conferências que ocorreram em horários distintos, havia sempre o mesmo número de pessoas assistindo a cada uma delas. Sabe-se que a metade dos que compareceram à primeira conferência não foi a mais nenhuma outra; um terço dos que compareceram à segunda conferência assistiu a apenas ela e um quarto dos que compareceram à terceira conferência não assistiu nem a primeira nem a segunda. Sabendo ainda que havia um total de 300 pessoas participando do ciclo de conferências, e que cada uma assistiu a pelo menos uma conferência, o número de pessoas em cada conferência foi:
a) 180
b) 80
*c) 156
d) 210
e) 96
Solução:
Veja o diagrama de Venn a seguir, que ilustra os dados do enunciado.
Nota: John Venn - matemático inglês - 1834 - 1923.
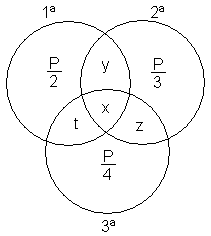
P/2 + x + y + t = P
P/3 + x + y + z = P
P/4 + x + z + t = P
Lembrando que o número total de pessoas é igual a 300, é lícito escrever também:
P/2 + P/3 + P/4 + x
+ y + z + t = 300
Efetuando todas as operações indicadas em relação a P nas equações acima
e arrumando, fica:
x + y + t = P/2
x + y + z = 2P/3
x + z + t = 3P/4
x + y + z + t = 300 – 13P/12
Substituindo o valor de x +
y + t = P/2 na equação x +
y + z + t = 300 – 13P/12, fica:
P/2 + z = 300 –
13P/12, de onde vem: z = 300 – 19P/12
Substituindo o valor de x + y + z =
2P/3 na equação x + y + z +
t = 300 – 13P/12, fica:
2P/3 + t = 300 – 13P/12, de onde vem: t = 300 – 21P/12
Substituindo o valor de x + z + t = 3P/4 na equação x + y + z + t = 300 –
13P/12, fica:
3P/4 + y = 300 – 13P/12, de onde vem: y = 300 – 22P/12
Substituindo os valores encontrados para y, z e t na equação
x + y + z + t = 300 – 13P/12, vem:
x + (300 – 22P/12) + (300 – 19P/12) + (300 – 21P/12) = 300 – 13P/12
Desenvolvendo e simplificando a expressão acima, vem:
x + 900 – 300 = 22P/12 + 19P/12 + 21P/12 – 13P/12
x + 600 = 49P/12
x = 49P/12 – 600
Em resumo:
x = 49P/12 – 600
y = 300 – 22P/12
z = 300 – 19P/12
t = 300 – 21P/12
Ora, como x, y, z e t referem-se a quantidade de pessoas, serão
necessariamente números inteiros e positivos ou seja: x > 0, y > 0,
z
> 0 e t > 0. Observe também que nas expressões de x, y, z e t acima,
sempre aparece o valor P dividido por 12, ou seja,
para que x, y, z e t sejam
inteiros, P deverá ser necessariamente um múltiplo de 12.
Então poderemos escrever:
49P/12 – 600 > 0 ,
logo, 49P/12 > 600 , logo,
49P > 7200 , logo, P > 7200/49 e, portanto
P > 146,93
Analogamente,
300 – 22P/12 > 0 ,
logo, 300 > 22P/12 ,
logo, 22P/12 < 300 ,
logo, 22P < 3600 e,
portanto P < 163,63
E, também,
300 – 19P/12 > 0 ,
logo, 300 > 19P/12 ,
logo, 19P/12 < 300 ,
logo, 19P < 3600 e,
portanto P < 189,47
E, finalmente,
300 – 21P/12 > 0 ,
logo, 300 > 21P/12 ,
logo, 21P/12 < 300 ,
logo, 21P < 3600 ,
e , portanto P < 171,42
Logo, o valor de P tem que ser inteiro e múltiplo de 12 e atender
simultaneamente às desigualdades P > 146,93
e P < 163,63
e
P < 189,47 e P < 171,42. Então,
o valor de P é um número múltiplo de 12, maior do que 146,93 e menor do que
163,63.
A sucessão de inteiros que satisfazem à segunda condição é:
147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162 ,
163.
Destes, o único que é múltiplo de 12 é 156,
que é a resposta do problema, ou seja, a alternativa correta é a de letra C.
Uma outra pergunta: quantas pessoas assistiram
às três conferências?
Agora é fácil: observando a figura abaixo, este número será igual a x.

Ora, já sabemos que P = 156 e x = 49P/12 – 600.
Então, substituindo, vem: x = 49.156/12 – 600 = 637 – 600 = 37
Portanto, 37
pessoas assistiram as três conferências.
Uma outra forma de solução
para este problema:
O problema acima foi enviado pelos Professores João Mesquita e
Carlos Gomes, de Natal –
Rio Grande do Norte – RN. Agradecemos aos diletos amigos a contribuição ao
site www.paulomarques.com.br
.
Vamos reproduzir a seguir, a solução do mesmo
problema apresentada pelos citados Professores.

A partir daí podemos escrever:
z = 300 - (P + P/3 + P/4) = 300 - 19P/12
t = 300 - (P + P/2 + P/4) = 300 - 7P/4
E ainda, x = P/2 - (y + t) = P/2 - (600 - 11P/6 - 7P/4) = 49P/12 - 600
Os números x, y, t, z representam inteiros; então P representa
um múltiplo de 12. Chamemos P = 12k
Daí,
y = 300 - 22k
z = 300 - 19k
t = 300 - 21k
x = 49k - 600
Mas, esses números são inteiros positivos, o que implica:
300 - 22k > 0 , logo k < 13,63
300 - 19k > 0, logo k < 15,78
300 - 21k > 0, logo k < 14,28
49k - 600 > 0, logo k > 12,24
O único inteiro com essa característica é k = 13 e, assim,
como P = 12k fica P = 12.13 = 156.
Carlos Gomes - João Mesquita
- novembro 2007, Natal -
RN
Agora
resolva os seguintes:
1
- Com base nos dados do problema anterior, qual o número de pessoas
que assistiram a apenas uma conferência?
Resposta: 169
2 - UNEB-1997 - Um minicurso foi dado em três dias. Feito
um levantamento nas listas de freqüência, observou-se que, em cada dia, o
número de presentes foi sempre o mesmo. No entanto, 5 participantes
frequentaram-no apenas no primeiro dia; 2, apenas no segundo; 1, apenas
no terceiro; 42, no primeiro e segundo dias e 40, nos três dias. O número de
presentes, no primeiro dia de curso, correspondeu a:
(01) 47
(02) 49
*(03) 50
(04) 54
(05) 56
Dica: não esqueça de desenhar o diagrama de
Venn (John Venn - matemático inglês - 1834 -
1923) para facilitar a solução.
Nota: este é bem mais direto e fácil, do que o
exercício que foi resolvido acima. (UNEB = Universidade do Estado da Bahia).
Resposta: 50 pessoas estiveram presentes no primeiro dia de curso.
Feira de
Santana, 01 de dezembro de 2007 – Paulo Marques
- revisado e ampliado em
01/03/2008.
VOLTAR