Tang@ - Sen@ = 1/12

---

Resolva a equação trigonométrica tg x – sen x = 1/12 em U = [0, 360º] .

Nota: o título acima, Tang@ - Sen@ = 1/12 (bastante sugestivo), constou de um e-mail que foi-me enviado por um visitante da página, o qual solicitou a solução e se identificou apenas como um vestibulando. Na verdade, o que se quer é resolver a equação: tangente do arco x menos o seno do arco x ,  igual a 1/12. 

Solução:

Esta equação aparentemente bem simples, tem uma solução muito trabalhosa.
Sabemos da Trigonometria que:

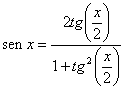
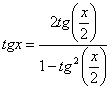
Nota 1: A solução que veremos a seguir é muito trabalhosa, mas, se você acompanhar o raciocínio desenvolvido, uma coisa é certa: você não vai adoecer por isto.

Nota 2: Esta questão foi enviada através e-mail, por um visitante da página que se identificou apenas como um vestibulando. Eta vestibulando danado de sabido!
Brincadeiras à parte, continuemos.

Fazendo tg(x/2) = y e substituindo na equação original o seno e a tangente em função da tangente do arco metade (veja as fórmulas acima), vem:



Vamos resolver a equação acima, lembrando que o MMC (mínimo múltiplo comum) dos denominadores é igual ao produto
12(1 – y²)(1 + y²)


Então, para y² ¹ 1, podemos suprimir os denominadores iguais, ficando:

12.(1 + y²).(2y) – 12.(1 – y²).(2y) = (1 – y²)(1 + y²)
24y.(1 + y²) – 24y.(1 – y²) = (1 – y²)(1 + y²)

Colocando 24y em evidencia, fica:
24y[(1 + y²) – (1 – y²)] = (1 – y²)(1 + y²)

24y.(1 + y² – 1 + y²) = (1 – y²)(1 + y²)
Desenvolvendo e simplificando ambos os membros, resulta:
48.y³ = 1 – y⁴

Nota: (1 – y²)(1 + y²) = 1² – (y²)² = 1 – y⁴

Logo,
48y³ =1 – y⁴
Igualando a zero, teremos:
y⁴ + 48y³ – 1 = 0
Esta equação possui 4 raízes reais ou complexas.

Não existe uma fórmula geral para resolver a equação acima.
Observe que nesta equação y⁴ + 48y³ – 1 = 0, se fizermos P(y) = y⁴ + 48y³ – 1, verificamos que 
P(0) = 0⁴ + 48.0³ – 1 = -1 < 0 e P(1) = 1⁴ + 48.1³ – 1 = 48 > 0.

Como P( 0 ) < 0 e P(1) > 0 , é óbvio que P(x) se anula no intervalo (0, 1), pois o valor da função P(x) mudou de
sinal (de menos (-) para mais (+)) quando x variou de 0 a 1.
Portanto, uma ou mais raízes da equação estarão no intervalo (0, 1).
Para achar uma solução aproximada sem recorrer a métodos iterativos que fogem ao nível do curso médio, vamos raciocinar da seguinte forma:

Seja P(y) = y⁴ + 48y³ – 1.
Já sabemos que P(y) se anula no intervalo (0,1), portanto existe uma raiz entre 0 e 1.
Vamos dividir o intervalo (0,1) de 0,10 em 0,10, por exemplo e calcular os seus valores.

y	P(y) == y4 + 48 y3 – 1
0,00	-1,0000
0,10	-0,9519
0,20	-0,6144
0,30	+0,3041
0,40	+2,0976
0,50	+5,0625
0,60	...
0.70	...
0,80	...
0,90	...
1,00	+48,0000

Observe que de y = 0,20 para y = 0,30 na tabela acima, P(y) mudou de sinal, o que quer dizer que pelo menos uma raiz estará entre estes valores, pois P(y) ao passar de (-) para (+), ela passará necessariamente pelo zero, ou seja, se anula.

Antes sabíamos que existia pelo menos uma raiz entre 0 e 1. Agora já restringimos mais o intervalo e sabemos agora que deve existir pelo menos uma raiz real entre 0,20 e 0,30. Vamos repetir o processo acima, dividindo o intervalo 0,20 a 0,30 de 0,02 em 0,02 por exemplo e calcular os valores de P(y).

y	P(y) = y4 + 48y3 – 1
0,20	-0,6144
0,22	-0,4865
0,24	-0,3331
0,26	-0,1518
0,28	+0,0598
0,30	+0,3041

Observe que de 0,26 para 0,28 houve uma nova mudança de sinal, indicando que a raiz está entre 0,26 e 0,28. Repetindo-se o processo, vem:

y	P(y) = y4 + 48y3 – 1
0,26	-0,1518
0,27	-0,0499
0,28	+0,0598

Observe que de y = 0,27 para y = 0,28 o valor de P(y) mudou de sinal ( de menos (-) para mais (+)). Portanto, a raiz deve estar entre 0,27 e 0,28, ou seja 0,27 < y < 0,28.

Poderíamos repetir o processo, agora dividindo o intervalo 0,27 a 0,28 de 0,001 em 0,001 e assim sucessivamente.

Encontrei o valor aproximado y @ 0,2747
Nota: para efetuar os cálculos das tabelas acima, utilizei uma calculadora científica.
A calculadora do windows serve.

Ora, como a equação y⁴ + 48y³ – 1 = 0 é do quarto grau, pela teoria das equações algébricas sabemos que ela possui 4 raízes reais ou complexas. Já achamos uma delas de valor aproximado 0,2747 (ou 0,2747001 com 7 decimais)
Abaixo, indicamos um programa freeware que resolve equações polinomiais, também conhecidas como equações algébricas.
Se você calcular os valores de P(y) = y⁴ + 48y³ – 1 para y = -48 e para y = -49, irá perceber que neste intervalo P(y) muda de sinal, ou seja:
P(-48) = (-48)⁴ + 48(-48)³ – 1 = 48⁴ – 48⁴ – 1 = - 1 < 0
P(-49) = (-49)⁴ + 48(-49)³ – 1 = 49⁴ – 49³.48 – 1 = 49³(49 – 48) – 1 = 117648 > 0
Então, deve existir outra raiz real no intervalo (-49, -48).
Utilizando o mesmo método visto anteriormente, encontraremos o valor aproximado
–48,0000092 para a segunda raiz real de P(y) = 0.

Existe um programa freeware – tamanho 114 kB – Polynomial Teacher – que resolve equações polinomiais ou equações algébricas.
Utilizando esse programa, obtive as seguintes raízes da equação y⁴ + 48y³ – 1 = 0:

Raízes reais: y₁ = 0,245 e y₂ = - 48,000
Raízes complexas: y₃ = -0,137 + 0,239i e y₄ = -0,137 – 0,239i
Observe que os resultados possuem apenas 3 casas decimais.
Aliás, o autor do software – Bob Terrell - adverte na tela de entrada do software que "Numerical accuracy is not garanteed" ou seja, "precisão numérica não é garantida" . Apesar disto, este freeware é uma "mão na roda" para achar as raízes aproximadas das equações algébricas também conhecidas como equações polinomiais.

As raízes reais – as que nos interessam no presente caso - são então:

y = 0, 2747001 ou y = - 48,0000092

Como no início do problema fizemos a mudança de variável tg(x/2) = y, vem, substituindo:

tg(x / 2) = 0,2747001 ou tg(x/2) = - 48,0000092
Temos que resolver estas duas equações trigonométricas que são do tipo tg a = tg b.
Já sabemos que : tg a = tg b Û a – b = k.180º onde k é um inteiro.

Usando uma tabela trigonométrica ou uma calculadora, encontramos:
tg (x/2) = 0,2747001 = tg 15,3602º ou tg (x/2) = - 48,0000092 = tg (-88,8065º)

Resolvendo a primeira equação:
tg (x/2) = tg 15,3602º
Então, como vimos acima, poderemos escrever:
(x/2) – 15,3602º = k.180º onde k é um inteiro.
Logo, x/2 = 15,3602 + k.180º
Tirando o valor de x, fica:
x = 2(15,3602º) + 2.k.180º
x = 30,7204º + k.360º, sendo k um número inteiro.

Resolvendo a segunda equação:
tg(x/2) = tg(-88,8065º)
Então, como vimos acima, poderemos escrever:
(x/2) – (-88,8065º) = k.180º
x/2 = k.180º - 88,8065º
Logo, x = 2.k.180º - 2.88,8065º
x = k.360º - 177,6130º , sendo k um número inteiro.

Portanto, em R – conjunto dos números reais – o conjunto solução da equação dada
tg x – sen x = 1/12 é igual a:
S = {x; x = 30,7204º + k.360º ou x = k.360º - 177,6130º , k Î Z}
Notas:
a) Z = conjunto dos números inteiros.
b) atribuindo-se valores inteiros a k, obteremos as raízes da equação trigonométrica dada.
c) é claro que em R – conjunto dos números reais – o conjunto solução da equação dada possui um número infinito de elementos.

Observe entretanto, que no enunciado da questão foi solicitado determinar as soluções no intervalo [0,360º]. Deveremos pois, atribuir valores convenientes a k, para encontrar as soluções que pertencem ao intervalo dado.

Teremos então:

Na primeira solução geral: x = 30,7204º + k.360º
k = 0 Þ x = 30,7204º + 0.360º = 30,7204º
Observe que para k = 1, obteremos uma raiz fora do intervalo dado, ou seja, 390,7204º.

Na segunda equação geral: x = k.360º - 177,6130º
k = 1 Þ x = 1.360º - 177,6130º = 182,3870º
Observe que para k = 0, obteremos uma raiz fora do intervalo dado, ou seja, -177,6130º

Portanto, o conjunto solução da equação dada no intervalo [0,360º] é igual a:
S = {30,7204º ; 182,3870º}
Paulo Marques, Feira de Santana - BA - 23 de setembro de 2003

---

VOLTAR