Vestibulares do Passado IV - Década de 50

A seguir, vamos resolver alguns problemas de vestibulares da década de 50 e até de 30! Matemática não tem idade!

Vejam estas preciosidades!. Quase do mundo antigo! eh eh ...

1 – Faculdade Nacional de Arquitetura – 1951

Numa progressão aritmética de número par de termos, a soma dos termos de ordem ímpar é 70 e a de ordem par é 85. A soma dos extremos é 31. Escrever essa progressão.

Solução: 

Seja a Progressão Aritmética - PA  :: a₁, a₂, a₃, ...
Sabemos que n é par, pelo enunciado da questão.
Podemos escrever,  segundo o enunciado:
a₁ + a₃ + a₅ + ... +  ... + a_2n-1  = 70 (soma dos termos de ordem ímpar). (Equação 1)
a₂ + a₄ + a₆ + ... + ... + a_2n = 85 (soma dos termos de ordem par). (Equação 2)

Somando membro a membro as duas igualdades acima, obteremos:
a₁ + a₂ + a₃ + a₄ + a₅ + ... + a_2n-1 + a_2n = 70 + 85 = 155 (Equação 3)

Ora, sendo 2n o número de termos da PA,  a soma dos termos do primeiro membro é igual a S_2n (soma dos 2n primeiros termos da progressão aritmética). 
Logo, S_2n = 155.

O problema nos diz que a soma dos extremos vale 31, ou seja: a₁ + a_2n = 31.

Usando a fórmula da soma dos termos de uma PA, vem:
S_2n = [(a₁ + a_2n).2n] / 2 \ 155 = (31.2n) / 2 \ 155 = 31n e, daí, vem que n = 5 .

Subtraindo a equação 1 da equação 2 , obteremos:
(a₂ – a₁) + (a₄ – a₃) + (a₆ – a₅) + ... + (a_2n – a_2n-1) = 85 – 70 = 15
(a₂ – a₁) + (a₄ – a₃) + ... +  ... = 85 - 70 = 15
Como a₂ – a₁ = a₄ – a₃ = ... = r = razão da PA , vem:
r + r + r + ... + r = 15
Já sabemos que n = 5 e, portanto, 5 termos iguais a r. Logo, vem:
5r = 15 \ r = 3 ( a razão da PA é igual a 3).
Para escrever a PA. , falta apenas achar o valor do primeiro termo a₁.

A partir de n = 5, a equação 3 acima pode ser escrita como:
a₁ + a₂ + a₃ + ... + a₉ + a₁₀ = 155

Como a_n = a₁ + (n-1).r, poderemos escrever a igualdade acima como:
a₁ + (a₁ + r) + (a₁ + 2r) + ... + (a₁ + 9r) = 155

E como são 10 termos, vem: (a₁ somado 10 vezes):

10.a₁ + (r + 2r + 3r + ... + 9r) = 155
10.a₁ + r(1+2+3+ ... + 9) = 155
Mas, 1+2+3+ ... + 9 = [(1 + 9)9] / 2 = 45

Logo, 10.a₁ + 45r = 155
Mas, já sabemos que  r = 3, logo:

10.a₁ + 45.3 = 155
10.a₁ = 155 - 135 = 20, de onde tiramos:  a₁ = 2

E como r = 3, a progressão aritmética procurada, será finalmente:
:: 2, 5, 8, 11, 14, 17, 20, 23, 26, 29.

Verificação:

Soma dos termos de ordem par = a₂ + a₄ + ...  = 5+11+17+23+29 = 85
Soma dos termos de ordem ímpar = a₁ + a₃ + ... = 2 + 8 +14 + 20 + 26 = 70

2 – Escola de Engenharia de Pernambuco – 2ª chamada – 1959

Determinar os valores inteiros de m que satisfazem a equação:

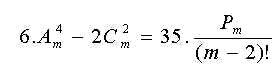
Solução: Temos, pelas fórmulas da Análise Combinatória:

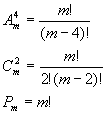
Substituindo na equação dada, vem:

Colocando m! em evidencia e simplificando, fica:

Observando que: (m-2)! = (m-2).(m-3).(m-4)! , e substituindo, vem:

Podemos escrever a igualdade acima como:

Multiplicando ambos os membros por (m-4)! , para m ¹ 4, vem:

Daí, vem:
6(m-2)(m-3) = 36 \ (m-2)(m-3) = 6 \ m² – 5m + 6 – 6 = 0
m² – 5m = 0 ou m(m-5) = 0, de onde vem: m = 0 ou m = 5.

A raiz m = 0 não serve, pois tornaria sem sentido o segundo membro da equação dada. Logo, o valor inteiro procurado é somente 
m = 5.

Resposta: m = 5

3 – Escola Fluminense de Engenharia – RJ – 1959
Componha a equação de menor grau possível e de coeficientes reais que tenha as raízes i e 2i.

Solução: 

Sendo i uma raiz, o seu conjugado (– i) também será raiz.
Sendo 2i a outra raiz, o seu conjugado (-2i) também será raiz. Logo, as raízes da equação procurada serão: i, - i, 2i e –2i. 

Daí, vem, que a equação de menor grau possível será dada por:
(x – i)[x – (- i)].(x – 2i).[x – (-2i)] = 0
(x – i)(x + i)(x –2i)(x + 2i) = 0

Desenvolvendo, vem:
(x² – i²)(x² – 4i²) = 0 e como i² = -1, substituindo, fica:
(x² + 1)(x² + 4) = 0

Efetuando a multiplicação dos dois binômios, vem:
x⁴ + 4x² + x² + 4 = 0
Simplificando, vem finalmente que a equação procurada é:

x⁴ + 5x² + 4 = 0

4 – Escola Nacional de Engenharia – 1931
Calcular a soma dos termos da progressão aritmética, :: 12, 19, ... desde o 25º até o 41º termo.

Solução: 

Temos: razão = r =19 – 12 = 7
a₂₅ = a₁ + (25 – 1).7 = 12 + 24.7 = 180 = vigésimo quinto termo.
a₄₁ = a₁ + (41 – 1).7 = 12 + 40.7 = 292 = quadragésimo primeiro termo.

A partir do 25º termo, a progressão fica:
:: ...180, 187, ... , 292, ...

A partir do 25⁰ até o 41⁰ termo, existem 41 – 25 + 1 = 17 termos. Logo, poderemos aplicar a fórmula da soma dos termos de uma PA, considerando 17 termos, a partir do 25⁰ até o 41⁰ termo.
Considerando-se esta nova PA de primeiro termo 180 e último termo 292, aplicando a fórmula da soma dos termos , teremos:



Nota : quantos números naturais existem de 46 a 125? Cuidado!
Existem 125 – 46 + 1 = 80 números naturais. (Não se esqueça nunca de somar uma unidade. Verifique!).

Resposta: 4012

5 – Escola Nacional de Química – 1952
Dada uma progressão aritmética cujo primeiro termo é 4 e o último é 46 e sabendo-se que a razão é igual ao número de termos, calcular a soma dos termos.

Solução: 

PA :: 4, ... , 46.
razão = r = n = número de termos.
Vamos aplicar a fórmula fundamental das progressões aritméticas:
a_n = a₁ + (n – 1)r \ 46 = 4 + (n – 1).n , já que n = r.

Daí, vem: 46 – 4 = n² – n \ 42 = n² – n \ n² – n – 42 = 0
Resolvendo a equação do 2º grau acima, encontramos n = 7 ou n = -6. A raiz negativa, evidentemente não serve (o número de termos não pode ser negativo).

Logo, o número de termos é igual a n = 7.

Portanto, a soma procurada, será igual a:


Resposta: 175

Paulo Marques, Feira de Santana - BA - editado em 20/11/2010.

VOLTAR