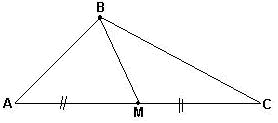
Pede-se resolver as seguintes questões:
1 – provar que BM = AM = MC
2 – supondo que a mediana BM seja igual à média geométrica dos catetos AB e BC, calcule o valor do cosseno do ângulo C.
Solução:
1 – Pelo teorema dos cossenos – TC poderemos escrever:

BC2 = BM2 + MC2 – 2.BM.MC.cos(BMC)
AB2 = BM2 + AM2 – 2.BM.AM.cos(BMA)
Como AM = MC, vem, substituindo na segunda igualdade:
AB2 = BM2 + MC2 – 2.BM.MC2.cos(BMA)
Observe que os ângulos BMC e BMA são suplementares ou seja: BMC + BMA = 180º .
Ora, sabemos da Trigonometria que se dois ângulos são suplementares então o cosseno de um deles é igual ao oposto do cosseno do outro ou seja: cos(BMA) = - cos(BMC).
Portanto, a igualdade anterior fica:
AB2 = BM2 + MC2 – 2.BM.MC.[- cos(BMC)] , ou seja:
AB2 = BM2 + MC2 + 2.BM.MC.cos(BMC)
Em resumo, temos então as seguintes igualdades:
BC2 = BM2 + MC2 – 2.BM.MC.cos(BMC)
AB2 = BM2 + MC2 + 2.BM.MC.cos(BMC)
Somando membro a membro as duas igualdades acima, resulta:
BC2 + AB2 = 2.BM2 + 2.MC2
Vejam que pelo teorema de Pitágoras, BC2 + AB2 = AC2, ou seja: a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Substituindo, fica: AC2 = 2.BM2 + 2.MC2
Lembrando que AC = 2.MC , pois M é ponto médio de AC, vem, substituindo:
(2.MC)2 = 2.BM2 + 2.MC2
Então, 4.MC2 = 2.BM2 + 2.MC2
Daí, 4.MC2 – 2.MC2 = 2.BM2
Então, 2.MC2 = 2.BM2
Ou, MC2 = BM2 e, como MC e BM são distâncias, são números positivos e, portanto, MC = BM. Ora, como MC = AM, vem finalmente que MC = AM = BM, o que queríamos provar.
Conclusão: em todo triângulo retângulo, o comprimento da mediana em relação à hipotenusa é igual à metade da hipotenusa. Convém guardar esta propriedade provada acima.
2 - supondo que a mediana BM seja igual à média geométrica dos catetos AB e BC, calcule o valor do cosseno do ângulo C.
Observe novamente o triângulo retângulo dado:

Nota: sabemos que se x é a média geométrica de y e z então x2 = y.z
No presente caso, teremos pelo enunciado: BM2 = AB.BC
Sejam as medidas BM = m, AB = b, BC = c e AC = a.
Podemos escrever, pelo resultado obtido no item 1 acima: m = a / 2.
Substituindo, fica: (a / 2)2 = b.c \ a2 / 4 = b.c \ a2 = 4.b.c
Pelo teorema de Pitágoras, sabemos que a2 = b2 + c2 (o quadrado da hipotenusa é igual à soma dos quadrados dos catetos).
Substituindo o valor de a2 = 4bc, fica:
4bc = b2 + c2
Dividindo ambos os membros por bc, vem:
(4bc / bc) = (b2 + c2) / bc = (b2 / bc) + (c2 / bc)
Simplificando, fica: 4 = (b / c) + (c / b) = (b / c) + 1 / (b / c)
Nota: c/b = 1/(b/c)
Temos então: 4 = (b/c) + 1/(b/c)

Ora, b / c = AB / BC = tg C (ver fig. acima) pois num triângulo retângulo, a tangente de um ângulo é igual à razão entre o cateto oposto e a hipotenusa.
Substituindo então, fica:
4 = tg C + 1/tg C
Já sabemos da Trigonometria que tg C = (sen C) / (cos C)
Substituindo na expressão acima, fica:
4 = (senC) / (cosC) + 1 / (senC)/(cosC)
E, portanto, 4 = (senC) / (cosC) + (cosC)/(senC)
Desenvolvendo a expressão acima, fica:
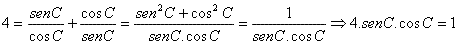
Nota: sen2C + cos2C = 1 (Teorema Fundamental da Trigonometria)
Ficamos então com a expressão: 4.senC.cosC = 1
Podemos escrever a expressão acima, da seguinte forma conveniente:
2.(2.senC.cosC) = 1
Lembrando da Trigonometria que 2senC. cosC = sen2C (seno do arco duplo), vem, substituindo:
2.sen2C = 1 \ sen2C = 1/2
Ora, 1/2 = sen30º
Então, sen2C = sen30º e, como C é um ângulo agudo, vem que 2C = 30º e, portanto,
C = 15º
O problema pede para calcular cosC ou seja, cos15º
Lembrando da Trigonometria que cos2C = 2cos2C – 1, vem, substituindo o valor de C=15º:
cos(2.15º) = 2.cos215º - 1
cos30º = 2.cos215º - 1
Como cos30º = Ö3 /2, vem: Ö3 /2 = 2.cos215º - 1 Þ 1 + Ö3 /2 = 2.cos215º
Portanto, cos215º = (1 + Ö3 /2 ) /2 = (1/ 2) + (Ö3 /4) = (2 + Ö3) /4
Ora, se A2 = B então A = ÖB , quando A é positivo. Então, da expressão anterior resulta:
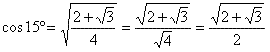
Usando uma calculadora (a do Windows serve) e efetuando o cálculo acima encontramos para o cosseno de 15 graus, o valor 0,9659, que pode ser obtido também diretamente através consulta à tábua trigonométrica, que normalmente comparece como apêndice de livros de Matemática do segundo grau.
Portanto
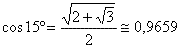
O problema então, terminou!
Paulo Marques, Feira de Santana – BA , 30 de setembro de 2006
VOLTAR