1) FEI /1968 - A igualdade 7x + 7x-1 = 8x se verifica:
a) apenas para valores irracionais de x
b) apenas para x = 1
c) para x=0 e x=1
d) para x=1 e x = -1
e) nenhuma das respostas anteriores
Solução:
Podemos escrever, colocando 7x em evidencia:
7x(1 + 1/7) = 8x
7x(8/7) = 8x
![]()
Portanto, alternativa correta: B
2) Se a função f é tal que f(senx) = (senx)2 , então f(x) é igual a:
a) cosx
b) tgx
c) x2
d) 1
e) cosecx
Solução:
Seja senx = t. Vem: f(t) = t2 . Logo, f(x) = x2 e, portanto, alternativa C.
3) Se sen4x + cos4x = 5/8 e 45º < x < 90º então calcule sen2x.
Solução:
Considere a relação fundamental da
Trigonometria:
sen2x + cos2x =1
Quadrando ambos os membros, vem:
(sen2x + cos2x)2
= 12
sen4x + 2.sen2x.cos2x+cos4x
= 1
sen4x + cos4x = 1 – 2sen2xcos2x
sen4x + cos4x = 1 – 2(senx.cosx)2
5/8 = 1 – 2(senx.cosx)2
Mas sen2x = 2senx.cosx Þ
senx.cosx = (sen2x) /2
Substituindo o valor de senx.cosx , vem:
5/8 = 1 - 2[((sen2x) /2]2
5/8 – 1 = - 2[(sen22x) / 4]
5/8 – 1 = - (sen22x) / 2
1 – 5/8 = (sen22x) /2
3/8 = (sen22x) /2 Þ
6/8 = 3/4 = sen22x Þ
sen2x = ± Ö
3 /2
Ora, como o enunciado do problema nos informa que
45º < x <
90º, concluímos que 90º <
2x < 180º
e portanto, o arco 2x é do 2º quadrante, onde sabemos que o
seno é positivo. Logo, a solução negativa não
serve e concluímos que o valor de sen2x é Ö
3 /2.
Portanto, sen2x = + Ö
3 / 2.
4) Se 102y = 25 então calcule 10 –y .
Solução:
Podemos escrever: (10y)2 =
25 Þ 10y
= 5, pois 52 = 25 e 10y >
0.
10y = 5 Þ
(10y) –1 = 5 –1Þ
10 –y = 1/5, pois 5-1 = 1 / 51 = 1/5.
Resp: 1/5
5) POLI 1959) Matemática não tem idade!
Determine o domínio da função
y = f(x) definida por:
![]()
Solução:
Sabemos que só existe logaritmo de número
positivo. Logo,
a expressão log
log y somente existirá se log y>
0.
Portanto, deveremos ter:
![]()
Obs: log B = log10B (logaritmo decimal
®
base 10) e log 1 = 0.
Para base maior do que 1, a função
logarítmica é crescente. Logo, concluímos:
![]()
![]()
Lembre-se que y / y = 1, para
y ¹ 0.
Podemos então escrever:
![]()
Temos uma inequação quociente a ser resolvida.
a) Raízes da equação do 2º
grau (numerador): –2x2 + 2x + 4 = 0
A equação é equivalente a 2x2
– 2x – 4 = 0 ou x2 - x - 2 = 0
Raízes 2 e -1. (Aplique a fórmula
de Bhaskara ou a forma (S,P) de uma equação do 2º grau).
b) Raízes da equação do 2º
grau x2 – 4x + 3 = 0
Raízes 3 e 1.
Ora, como sabemos que se o trinômio ax2+bx+c
possui raízes x1 e x2 , podemos escrever:
ax2+bx+c = a(x-x1)(x-x2),
teremos então:
![]()
Que é equivalente a:
![]()
Obs: o sinal da desigualdade mudou, porque multiplicamos ambos os membros por –1/2 para eliminar o número (-2) do numerador. Sabemos que ao multiplicarmos ambos os membros de uma desigualdade por um número negativo, ela muda de sentido.
Para resolver a inequação quociente
acima, vamos estudar os sinais de cada binômio presente na desigualdade
acima, através de uma tabela de sinais.
Para entender a tabela abaixo, basta lembrar das
regras de multiplicação e divisão de números
relativos.
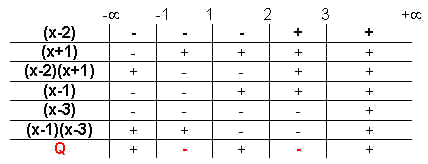
Portanto, os valores que satisfazem a última
desigualdade acima , são:
-1 <
x < 1 ou 2<
x < 3 onde o quociente
Q é negativo.
Portanto, o domínio da função
será:
D = {x Î
R; -1 < x <
1 ou 2 < x <
3}
A resposta acima poderá também ser
escrita na forma de intervalo:
D = (-1, 1) È
(2, 3)
Paulo Marques - Feira
de Santana - BA - 07 de setembro de 1996