| Vestibulares do Brasil I |
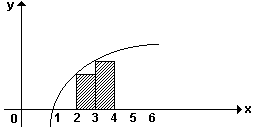
| UFGO 1984 - Se a curva da figura representa o gráfico da função y = log x, onde x é um número positivo, calcule o valor da área hachurada. |
SOLUÇÃO:
| Como a função
é y = log x, teremos, da simples observação do
gráfico acima: x = 2 Þ y = log 2 x = 3 Þ y = log 3 Observe que o primeiro retângulo possui medida da base igual a 3 - 2 = 1 e altura igual a log 2. Analogamente, o segundo retângulo possui a medida da base igual a 4 - 3 = 1 e altura igual a log 3. Como a área de um retângulo é igual ao produto da base pela altura, teremos, para os dois retângulos: S = (1 . log 2) + (1 . log 3) = log 2 + log 3 Portanto, S = log 2 + log 3 Ora, sabemos que o logaritmo de um produto, é igual à soma dos logaritmos, isto é: log (A . B) = log A + log B Portanto, log A + log B = log ( A . B) Logo, log 2 + log 3 = log (2 . 3) = log 6 Então, a resposta procurada será S = log 6 Para revisar LOGARITMOS, clique AQUI. Para retornar, clique em VOLTAR no seu browser. |
| UNESP 2000 - Duas plantas de mesma espécie, A e B , que nasceram no mesmo dia, foram tratadas desde o início, com adubos diferentes. Um botânico mediu todos os dias o crescimento, em centímetros, destas plantas. Após 10 dias de observação, ele notou que o gráfico que representa o crescimento da planta A é uma reta passando por (2, 3) e o que representa o crescimento da planta B pode ser descrito pela lei matemática |
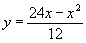
| Um esboço desses gráficos está apresentado na figura |
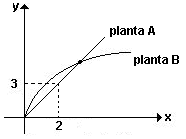
| Determine: a) a equação da reta b) o dia em que as plantas A e B atingiram a mesma altura e qual foi essa altura. |
SOLUÇÃO:
| a) a reta passa
pelos pontos (0, 0) e (2, 3). Ora, uma reta que passa pela origem, tem equação do tipo y = m . x, onde m é o coeficiente angular da reta. Podemos escrever para o ponto (2, 3) : 3 = m . 2 \ m = 3 / 2 Logo, a equação da reta procurada será: y = m . x = (3 / 2) . x Então, y = (3 / 2) . x \ 2y = 3x ou 3x - 2y = 0, que é a equação da reta procurada. b) As plantas A e B atingirão a mesma altura no ponto de interseção das duas curvas indicadas. Como as equações são conhecidas, igualando os valores de y nas duas equações, vem: |
![]()
| Como x2
- 6x = 0, vem: x ( x - 6) = 0 \ x = 0 OU x = 6. Como x representa o número de dias, teremos que as plantas atingirão a mesma altura no sexto dia. A altura de ambas as plantas será então y = (3 / 2) . x = (3 / 2) . 6 = 9 Logo, as plantas terão a mesma altura no 6º dia e essa altura será igual a 9 cm. |
| UFBA 1996 - Numa progressão geométrica, o primeiro termo é igual a 7500, e o quarto termo é igual a 20% do terceiro. Determine o quinto termo da progressão. |
SOLUÇÃO:
| Pelo enunciado
do problema, podemos escrever a seguinte PG: :: 7500 ; a2 ; a3 ; 0,20. a3 ; a5 ; ... , na qual o quarto termo é igual a 20% = 0,20 do terceiro termo, ou seja: a4 = 0,20 . a3 \ a4 / a3 = 0,20. Como sabemos que a razão de uma PG é igual ao quociente da divisão entre um termo e o outro imediatamente anterior, podemos concluir que a razão dessa PG será igual a 0,20 - resultado do quociente da divisão do quarto pelo terceiro termo. Para calcular o quinto termo, basta usar a fórmula do termo geral de uma PG: a5 = a1 . q n - 1 = 7500 . (0,20) 5 - 1 = 7500 . (1 / 5)4 = 7500 / 54 Portanto, teremos: a5 = (75 . 100) / 54 = (3 . 52 . 100) / 54 = (3 . 100) / 52 = 300 / 25 = 60 / 5 = 12 Portanto, o quinto termo da PG é igual a 12. Para revisar PROGRESSÃO GEOMÉTRICA, clique AQUI. Para retornar, clique em VOLTAR no seu browser. |
| UCSal 1996 - Dividindo o polinômio f = -2x3 + 4x2 + k x + t, onde k, t Î R, por x + 1, obtém-se resto 12. Se f é divisível por x - 2 , então k + t é igual a: |
SOLUÇÃO:
| Na divisão de
um polinômio P(x) por x - a , o resto da divisão é
igual a P(a). Observe que x + 1 = x - (- 1) Logo, podemos escrever, considerando o polinômio f dado: 12 = f (- 1) = -2(-1)3 + 4(-1)2 + (-1).k + t 12 = 2 + 4 - k + t 12 - 2 - 4 = t - k t - k = 6 (igualdade 1) Como f é divisível por x - 2 , pelo mesmo
raciocínio anterior, teremos, considerando que neste
caso, o resto é igual a zero, já que f é divisível
por x - 2 : Para revisar POLINÔMIOS, clique AQUI. Para retornar, clique em VOLTAR no seu browser. |
| UFRN 1996 - Determine o valor de k na equação 2.22.23. ... . 2400 = 2k |
SOLUÇÃO:
| Considerando-se
o produto de potências de mesma base do primeiro membro
da igualdade dada, poderemos escrever: 2 (1+2+3+ ... + 400) = 2 k Portanto, 1 + 2 + 3 + ... + 400 = k Para determinar o valor de k, basta calcular a soma dos termos da progressão aritmética do primeiro membro, a qual possui primeiro termo igual 1, último termo igual a 400 e número de termos igual a 400. Logo, |
![]()
| UFRN 1996 - Quantos números de telefones com prefixo 231 existem em Natal, com todos os dígitos distintos e o último dígito igual ao dobro do penúltimo? Considere que os telefones de Natal tem números com 7 dígitos. |
SOLUÇÃO:
| Os números de
telefones são do tipo 2 3 1 X Y Z W Com a condição de que W = 2Z (o último dígito igual ao dobro do penúltimo), conforme enunciado do problema. O enunciado do problema diz também que todos os dígitos são distintos, portanto, para as posições desconhecidas, não poderemos utilizar os números 1, 2 ou 3, que já constam no prefixo. Observe que sendo W = 2Z, e como os números dos telefones possuem 7 dígitos, o dígito W será um número com 1 algarismo apenas ; isto elimina a possibilidade de termos Z = 5, 6, 7, 8 ou 9, pois neste caso, o dobro não teria apenas um algarismo. Além disto, Z não poderá ser igual a 1, 2 ou 3, senão teríamos dígitos repetidos, o que não é permitido. Restam então para Z os valores 0 ou 4. 0 (zero) não é possível, pois o dobro seria zero e, haveria repetição, o que não é permitido pelo enunciado da questão. Resta então a única alternativa possível para Z que é 4. Ou seja, Z = 4, o que implica que W sendo o dobro de Z, será igual a 8. Temos então: Z = 4 e W = 8. Os números dos telefones, serão então, da forma: 2 3 1 X Y 4 8 Como não
podemos ter dígitos repetidos, os dígitos X e Y somente
poderão ser escolhidos entre 0, 5, 6, 7 ou 9, num total
de 5 valores possíveis. Para revisar ANÁLISE COMBINATÓRIA, clique AQUI. Para retornar, clique em VOLTAR no seu browser. |
| UNIFOR 1995 - As raízes da equação x3 + 3x2 + k x - 8 = 0 onde k Î R, formam uma progressão aritmética. Determine o valor de k. |
SOLUÇÃO:
| Sendo r a razão
da PA, poderemos dizer que as raízes serão x - r , x e
x + r . A soma das raízes será então: S = (x - r) + x + (x + r) = 3x Pelas Relações de Girard, poderemos escrever: S = 3x = - 3/1 \ x = -1. Logo, as raízes da equação dada serão: x1 = - 1 - r = - (1 + r) x2 = - 1 x3 = - 1 + r = r - 1 Ainda pelas Relações de Girard, o produto P das raízes será igual a: P = x1 . x2 . x3 = -(- 8 / 1) = 8 = [-(r + 1)] (- 1) (r - 1) = (r + 1)(r - 1) = 8 (r + 1) (r - 1) = 8 r2 - 1 = 8 r2 = 9 Daí, vem : r = 3 ou r = -3. Portanto,
como as raízes são: Para revisar EQUAÇÕES ALGÉBRICAS, clique AQUI. Para retornar, clique em retornar no seu browser. |
| UNESP 2000 - Numa cidade com 30000
domicílios, 10000 domicílios recebem regularmente o
jornal da loja de eletrodomésticos X, 8000 recebem
regularmente o jornal do supermercado Y e metade do
número de domicílios não recebe nenhum dos dois
jornais. Determine: a) o número de domicílios que recebem os dois jornais. b) A probabilidade de um domicílio da cidade, escolhido ao acaso, receber o jornal da loja de eletrodoméstico X e não receber o jornal do supermercado Y. |
SOLUÇÃO:
| a) Veja a figura abaixo: |
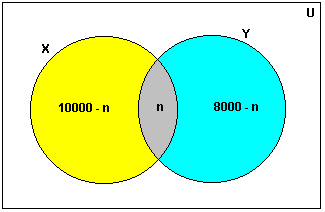
| Seja n o número
de pessoas que recebem os dois jornais: Teremos: 10000 - n + n + 8000 - n + 15000= 30000 Logo, 33000 - n = 30000 \ n = 3000. Portanto, 3000 domicílios recebem os dois jornais. b)nas condições do enunciado, existem
10000 - n = 10000 - 3000 = 7000 |
Paulo Marques, Feira de Santana - 24 de dezembro de 1999 - ampliado em 04/01/2007.