Determine a expressão simplificada do desenvolvimento do
somatório a seguir:
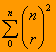
Solução:
Sabemos da fórmula do desenvolvimento de um Binômio de Newton do tipo (a + b )n ,
que:
(a + b)n = Cn,0 .
an + Cn,1.a n-1.b + Cn,2.a n-2.b2
+ Cn,3.a n-3.b3 + ... +
Cn,k.xn-k + ... + Cn,n.bn
No caso particular de
a = x
e b = 1, poderemos
escrever, substituindo os valores:
(x + 1)n = Cn,0 . xn + Cn,1.x n-1
+ Cn,2.x n-2 + Cn,3.x n-3 + ... + Cn,k.xn-k +
... + Cn,n-1.x + Cn,n
Poderemos escrever a relação acima, de “trás p’ra frente” ,
como:
(x + 1)n = Cn,n + Cn,n-1.x + Cn,n-2.x2
+ Cn,n-3.x3 + ... + Cn,n-n.xn
Sabemos da Análise Combinatória
que:
Cn,k = Cn,n-k (Propriedade dos
Números Binomiais complementares)
Portanto, teremos:
Cn,n-1 = Cn,1
Cn,n-2 = Cn,2
Cn,n-3 = Cn,3
.................
e, assim sucessivamente.
Substituindo na igualdade acima, vem que:
(x + 1)n = Cn,0 + Cn,1.x
+ Cn,2.x2 + Cn,3.x3 + ... + Cn,n.xn
Temos então, em resumo,
as duas igualdades abaixo, apenas reescritas, para facilitar o
acompanhamento:
(x + 1)n = Cn,0 . xn + Cn,1.x n-1
+ Cn,2.x n-2 + Cn,3.x n-3 + ... + Cn,k.xn-k +
... + Cn,n-1.x + Cn,n
(x + 1)n = Cn,0.x0
+ Cn,1.x1 + Cn,2.x2 + Cn,3.x3
+ ... + Cn,n.xn
Considerando que xn
. x0 = xn-1.x1 = xn-2.x2
= ... = xn , concluímos que se multiplicarmos as duas expressões
acima, membro a membro, obteremos para o coeficiente de xn, no
segundo membro, a soma:
(Cn,0)2 + (Cn.1)2
+ (Cn,2)2 + (Cn,3)2 + ... + (Cn,n)2
Para o produto dos primeiros membros, obteremos
evidentemente:
(x + 1)n . (x + 1)n = (x + 1)2n
O problema agora é determinar o coeficiente de xn
, no desenvolvimento do Binômio de Newton
(x + 1)2n .
Ora, sabemos que o termo geral do desenvolvimento de um binômio
(a + b)m é dado por:
![]()
Como no nosso caso m = 2n , a = x e b = 1,
vem:
![]()
Para obter xn na igualdade acima, deveremos
ter 2n – p = n \ p = n.
Fazendo então p = n na igualdade acima, obteremos:
![]()
Observe que 1p = 1n = 1.
Das inferências ou deduções acima, concluímos
inevitavelmente que:
![]()
Ora
companheiros estudantes. Se vocês conseguiram entender o desenvolvimento do
exercício, até aqui, o resto é fácil,
senão vejamos:
O problema pediu para determinar o somatório e, portanto,
vem finalmente que:
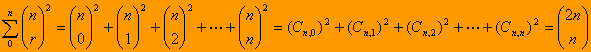
Nota: O
símbolo de somatório
Considere a seqüência <an>
= (a1, a2, a3, a4, ... , an
, ...)
A soma dos n primeiros termos
da seqüência acima, seria expressa por:
Sn = a1 +
a2 + a3 + a4 + ... + an
A soma acima, pode ser reescrita de uma forma mais compacta e bastante útil, utilizando a notação de somatório, conforme indicado abaixo:
![]()
Onde S é a letra grega sigma (maiúscula) e o símbolo acima deve ser lido como: somatório de todos os ai com i variando de 1 a n.
Os valores de i são denominados limites inferior e superior do somatório. No presente caso, o limite inferior é 1 e o limite superior é n.
Assunto para revisão:
Binômio de Newton
Paulo Marques - Feira de Santana - BA - 18 de Setembro de 2000 - atualizado em 16/01/2005.