UFBa 2002 - 1ª Fase    Num labirinto de um condomínio na UFBa

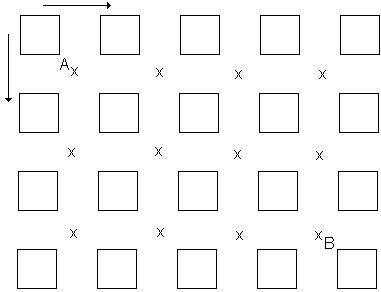
Na figura abaixo, cada quadrado representa um quarteirão de um condomínio e, em cada cruzamento de ruas indicado por um x, foi instalado um semáforo, exceto em A  e B. Um carro desloca-se de A para B, obedecendo as seguintes condições:

1.     o trajeto deve ser formado por segmentos de reta ligando pontos de cruzamentos  consecutivos;

2.      cada segmento só pode ser percorrido num dos dois sentidos indicados pelas setas na figura;

3.      o tempo gasto para percorrer cada segmento é de 2 minutos;

4.      cada semáforo, após ligado, funciona alternando apenas os sinais verde e vermelho, que ficam acesos por períodos de 3 e 2 minutos, respectivamente;

5.     o carro pára em cada semáforo que estiver fechado e parte no exato instante em que este abrir.

 Com base nessas informações, é correto afirmar:


(01) Existem 10 trajetos possíveis.

(02) Se os semáforos estiverem desligados, o tempo gasto pelo carro através de qualquer dos caminhos possíveis é igual a 8 minutos.

(04) Se os semáforos forem ligados ao mesmo tempo, e o carro partir de A, no instante em que os semáforos abrirem, serão gastos pelo menos 12 minutos no trajeto.

(08) Se os semáforos forem ligados de modo aleatório, então o tempo gasto pelo carro, será no máximo, 18 minutos.

(16) Sendo constante a distância entre dois cruzamentos consecutivos quaisquer, então a distância total percorrida pelo carro dependerá do trajeto. 

Solução:

Análise da proposição (01)

(01) Existem 10 trajetos possíveis.

Indicando por V o deslocamento vertical para baixo e H o deslocamento horizontal para a direita (tipos de deslocamentos possíveis, conforme o enunciado), teremos as seguintes disposições possíveis:

VHVHH        HHHVV     VHVHH    etc

Observe que, em qualquer caso, existem 3 deslocamentos do tipo H e 2 deslocamentos do tipo V. Temos então que calcular o número total de permutações com repetição, dos dois elementos V e H, com 3 repetições possíveis para H e duas repetições possíveis para V. Como são 5 posições possíveis, teremos:

Logo, existem 10 trajetos possíveis e esta proposição (01) é VERDADEIRA.


Análise da proposição (02)

(02) Se os semáforos estiverem desligados, o tempo gasto pelo carro através de qualquer dos caminhos possíveis é igual a 8 minutos.

Com todos os semáforos desligados, o carro poderá se deslocar de A até B sem parar em nenhum ponto. Como são cinco deslocamentos possíveis para alcançar o ponto B, teremos por simples multiplicação: Tempo = 5 . 2 = 10 minutos, já que o tempo gasto para percorrer cada segmento é, pelo enunciado, igual a  2 minutos.

Logo,  a proposição (02) é FALSA.

Análise da proposição (04)

(04) Se os semáforos forem ligados ao mesmo tempo, e o carro partir de A, no instante em que os semáforos abrirem, serão gastos pelo menos 12 minutos no trajeto.

Supondo uma trajetória típica (entre as 10 possíveis, conforme visto na resolução do item (01) acima), do tipo HHHVV, por exemplo, e lembrando que o tempo gasto para percorrer cada segmento é de  2 minutos,  que o sinal verde permanece 3 minutos aberto, que o sinal vermelho permanece 2 minutos fechado, que  o sinal alterna entre aberto e fechado,  e sendo P o tempo que o carro permanece parado aguardando o sinal abrir (ficar verde), poderemos raciocinar como segue:

Ora, como o sinal leva 3 minutos em verde e 2 minutos em vermelho, o sinal fechará aos 3 minutos e, portanto, no 4º minuto, o sinal estará fechado e levará mais 1 minuto fechado, tempo no qual o carro ficará parado. O sinal vai abrir e levará 3 minutos abertos, fechando na posição 7. Como o carro percorre um segmento em 2 minutos, ele encontrará no ponto 8 o sinal fechado e permanecerá mais 1 minuto parado. Então, o tempo total será igual a 4 + 1 + 4 + 1 + 2 = 12 minutos e, portanto, a proposição (04) é VERDADEIRA.

Análise da proposição (08)

(08) Se os semáforos forem ligados de modo aleatório, então o tempo gasto pelo carro, será no máximo, 18 minutos.

Ora, pelo enunciado do problema, o semáforo só possui dois estados: aberto – A  ou fechado – F . Como são 4 semáforos em qualquer um dos percursos escolhidos (basta observar a figura dada no enunciado), teremos os seguintes agrupamentos possíveis, no caso dos semáforos serem ligados de modo aleatório: AAAA,  AAFF, FFFF, etc.

Somente a título ilustrativo, verificamos que existem 16 agrupamentos possíveis, obtido do cálculo do número de arranjos com repetição dos elementos A e F associados com taxa 4, ou seja:

AR_n,k = n^k = 2⁴ = 16

A situação mais crítica, no caso aleatório, será o arranjo FFFF, onde o carro encontrará todos os 4 sinais fechados, gastando 2 minutos parados em cada um deles. Logo, supondo esta condição mais crítica, o tempo total de percurso poderá chegar a T_max = 10 minutos + 4.2 minutos = 18 minutos.

Portanto, a proposição (08) é VERDADEIRA.

Análise da proposição (16)

(16) Sendo constante a distância entre dois cruzamentos consecutivos quaisquer, então a distância total percorrida pelo carro dependerá do trajeto. 

Ora, sendo o percurso total sempre composto de 5 movimentos, conforme pode-se inferir da figura dada no enunciado, conclui-se que a distancia total percorrida independerá do trajeto, sendo portanto, esta proposição FALSA.

Deverá ser marcado no cartão de respostas a soma dos números associados às questões VERDADEIRAS, ou seja: 01 + 04 + 08 = 13 .

Paulo Marques – Feira de Santana – BA – 08 de janeiro de 2002. 

VOLTAR
CONTINUAR