Curiosidade II

Qual o valor de 0,99999999999999... ?
Vamos igualar a x.
x = 0,99999999999...
Multiplicando ambos os membros por 10 e 100 respectivamente, vem:
10x = 9,999999999...
100x = 99,999999999...
Subtraindo membro a membro, vem:
100x - 10x = 99,9999... - 9,9999...

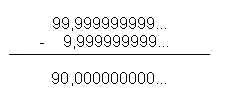
Logo, 90x = 90
Portanto, x = 90/90 Þ x = 1.

Outra forma: Sabemos que 1/3 = 0,3333...
Multiplicando ambos os membros da igualdade acima por 3, o que não altera a igualdade, uma vez que A=B Þ k. A = k . B, para kÎ R, vem:
3.(0,3333...) = 3. (1/3)
De onde se conclui inevitavelmente que:
0,9999... = 3/3 = 1.

Portanto: 0,9999999999999... = 1 (! ! !)

Qual a solução da equação (2x)^0,9999... = 4?
Ora, podemos escrever: (2x)¹ = 4 e, daí vem: 2x = 4 e portanto x = 2.

Paulo Marques - Feira de Santana - BA - 17 de abril de 1998

VOLTAR