| Numa certa loja de discos do planeta Terra |
Uma loja de discos classificou seus CDs em três tipos A, B e C, unificando o
preço para cada tipo. Quatro consumidores fizeram compras nessa loja nas
seguintes condições:
O primeiro comprou 2 CDs do tipo A, 3 do tipo B e 1 do tipo C, gastando
R$121,00.
O segundo comprou 4 CDs do tipo A, 2 do tipo B e gastou R$112,00.
O terceiro comprou 3 CDs do tipo A, 1 do tipo C e gastou R$79,00.
O quarto comprou 1 CD de cada tipo. Calcule quanto o quarto consumidor pagou à
loja.
Nota: CD = abreviatura de compact disk, o substituto do disquete.
Certamente aparecerá em breve o substituto do CD!
Solução:
Sejam a , b e c os preços unitários dos CDs dos tipos A, B e C
respectivamente.
Poderemos escrever, de acordo com o enunciado:
2a + 3b + c = 121
4a + 2b = 112
3a + c = 79
O problema pediu para calcular o valor consumido pelo quarto comprador. Como ele
comprou 1 CD de cada tipo, o valor gasto é igual a 1.a + 1.b + 1.c = a + b + c.
Observe que temos acima um sistema linear de 3 equações e 3 incógnitas, o
qual pode ser reescrito na forma:
2a + 3b + 1c = 121
4a + 2b + 0c = 112
3a + 0b + 1c = 79
Poderíamos aplicar o método de
escalonamento ou a regra
de Cramer para a solução do sistema acima. Mas, neste caso,
ganharemos mais tempo usando o método de substituição, tirando o valor de c
na terceira equação e substituindo na primeira.
Tirando o valor de c na terceira equação: c = 79 – 3 a .
Substituindo o valor de c na primeira equação: 2a + 3b + (79 – 3a) =
121
Simplificando, fica: 2a + 3b + 79 – 3a = 121 Þ 3b
– a = 121 – 79 = 42
Ou seja: 3b – a = 42
Tirando o valor de a na igualdade acima e substituindo na segunda
equação do sistema linear acima, fica:
3b – 42 = a Þ 4(3b – 42) + 2b = 112
Fica: 12b – 168 + 2b = 112
14b = 280 Þ b = 280 /
14 = 20
Então, a = 3b – 42 = 3.20 – 42 = 60 –
42 = 18 e, finalmente,
c = 79 – 3a = 79 – 3.18 = 79 – 54 = 25
Logo, a = 18, b = 20 e c = 25.
Portanto, o quarto consumidor gastou a + b + c = 18 + 20 + 25 = 63
Logo, ele gastou R$63,00.
Notas:
1 – o engraçado é que um estudante enviou-me esta questão por e-mail de
seguinte teor:
"Olá Paulo! Visitei o seu site e achei o conteúdo importante. Gostaria
que me ajudasse a resolver esta questão, pois tentei pelo diagrama
de Venn e não consegui. Agradeço desde já".
2 – diagrama de Venn = representação de um conjunto dado através de uma
curva plana fechada. Idéia atribuída a John Venn – matemático inglês (1834
– 1923). Observem que aplicar o conceito de diagrama de Venn para resolver a
questão acima, não seria uma boa idéia.
Exemplo de diagrama de Venn:
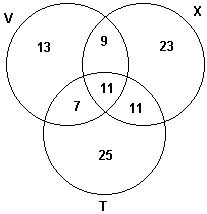
Nota: no diagrama de Venn acima, por exemplo, podemos visualizar
imediatamente que o conjunto
V U X U T possui 13 + 7 + 9 + 11 + 23 + 11 + 25 = 99 elementos.
(o símbolo U significa união).
Podemos visualizar também, por exemplo, que o conjunto V Ç
X Ç T possui 11 elementos.(o símbolo
Ç significa
intersecção).
Podemos visualizar por exemplo, que o conjunto V Ç
X possui 9 + 11 = 20 elementos.
Podemos visualizar também, por exemplo, que o conjunto T - (V U
X) possui apenas 25 elementos.
3 – caso utilizássemos aqui o método
de escalonamento ou a regra
de Cramer para a solução deste problema, gastaríamos muito
mais tempo. Tomar a decisão certa quanto à metodologia a ser aplicada na
solução de uma questão, é muito importante, pois nos exames vestibulares, o
tempo é uma variável preciosíssima, decidindo às vezes, a sorte do
vestibulando. Isto não quer dizer, de forma nenhuma, que os métodos acima são
inadequados. Aliás, são métodos poderosíssimos para a solução de Sistemas
Lineares. Ocorre que neste problema, ambos os métodos não
seriam os mais adequados, uma mera questão pontual, ou seja, uma mera questão
particular desse problema proposto.
4 - Imagine por exemplo que você vai fazer uma prova com 80 questões
propostas, de duração total 4 horas.
Ora, como 4 horas = 4.60 = 240 minutos, você disporá de 240/80 = 3 minutos
para resolver cada questão.
O segredo para um bom resultado na prova é não ultrapassar os 3 minutos para a
solução de cada questão. Se você perceber que não vai conseguir resolver a
questão neste tempo, o mais prudente é passar para a próxima.
Empacar (ou seja, ficar e não prosseguir) numa única questão, tem eliminado
muita gente de vestibulares.
É claro, que se você conseguir resolver a questão em 2 minutos, por exemplo,
a próxima poderá ser resolvida em até 3 + 1 = 4 minutos, usando o minuto que
você ganhou na questão anterior. Portanto, achar o melhor caminho para resolver uma questão, logo no
início, é fundamental e estratégico para um bom desempenho. Claro que estas
assertivas são óbvias, mas, muita gente se esquece desses detalhes simples.
Paulo Marques, 27 de setembro de 2003 – Feira de
Santana – BA.
VOLTAR
Página inicial