Matriz de Vandermonde

Chama-se matriz de Vandermonde a toda matriz quadrada de ordem n x n , ou seja, com n linhas e n colunas, da forma geral:

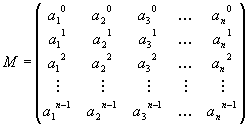
Matriz de Vandermonde com n linhas e n colunas.

Nota: Alexandre Vandermonde - músico e matemático francês do século XVIII - 1735/1796.
 
Observe que na matriz de Vandermonde acima, temos:
a) a primeira linha é composta por bases do tipo a_i (i Î N , conjunto dos números naturais) elevado a zero, ou seja, a₁, a₂, ... , a_n elevadas ao expoente zero e portanto são todas iguais a 1, pois a⁰ = 1 para todo a Î R , conjunto dos números reais.
b) a segunda linha é composta por bases do tipo a_i elevado à unidade, ou seja, a₁, a₂, ... , a_n elevadas ao expoente um e portanto são todas iguais a si próprio, pois a¹ = a para todo a Î R. Sendo assim, a matriz genérica acima pode ser reescrita na forma abaixo:

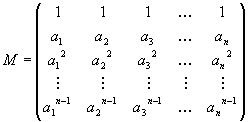
Numa matriz de Vandermonde, os elementos a₁, a₂, a₃, ... , a_n são denominados elementos característicos da matriz. Assim por exemplo, na matriz de Vandermonde abaixo,

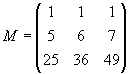
os elementos característicos são 5, 6 e 7. Observe que a matriz é de Vandermonde pois na terceira linha os elementos são obtidos da segunda linha, quadrando cada termo, ou seja:
25 = 5², 36 = 6² e 49 = 7².

Prova-se que o determinante de uma matriz de Vandermonde pode ser obtido multiplicando-se todas as diferenças possíveis entre os elementos característicos (a_i – a_k) com a condição de que i > k. Assim, por exemplo, na matriz M acima, o determinante será igual a :
|M| = (6 – 5).(7 – 6).(7 – 5) = 1.1.2 = 2.

Veja mais um exemplo: Calcule o determinante de Vandermonde abaixo:

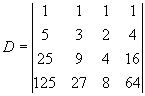
Ora, como os elementos característicos são 5, 3, 2 e 4, o determinante será igual a:
|D| = (3 – 5).(2 – 5).(2 – 3).(4 – 5).(4 – 3).(4 – 2) = (-2).(-3).(-1).(-1).1.2 = 12.

Claro que este método de cálculo de determinantes, aplica-se somente a matrizes de Vandermonde.

Nota: como o determinante de Vandermonde é obtido multiplicando-se todas as diferenças possíveis (a_i – a_k) entre os elementos característicos, com a condição que i > k, podemos concluir que se pelo menos dois dos elementos característicos forem iguais entre si, o determinante será nulo, pois aparecerá um zero no produto.

Exemplo:


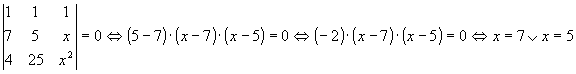
Então, se x for igual a 5 ou a 7, o determinante de Vandermonde acima, será nulo.

Exercício resolvido:
Calcule o determinante a seguir:


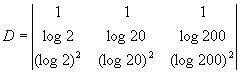
Solução:

Repare que trata-se de um determinante de Vandermonde, cujos elementos característicos são log2, log20 e log200. Então, pelo que já vimos, o determinante será igual a:
D = (log20 – log2).(log200 – log2).(log200 – log20)
Aplicando a propriedade de logaritmo de quociente, vem:
D = log(20/2).log(200/2).log(200/20) = log10.log100.log10 = 1.2.1 = 2
Resposta: D = 2

Nota: lembre-se que log(A/B) = logA – logB , para A e B positivos e, portanto, reciprocamente, logA – logB = log(A/B).

Agora resolva este:

Calcule o determinante:

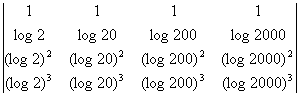
Resposta: 12

Nota: observe que trata-se de um determinante de Vandermonde, cujos elementos característicos são log2, log20, log200 e log2000. Assim, basta efetuar o produto seguinte:
(log20 – log2).(log200 – log2).(log200 – log20).(log2000 – log2).(log2000 – log20).(log2000 – log200).

Paulo Marques, 03 de abril de 2004 – Feira de Santana – BA. Editado em 18/06/2011.

                                                            VOLTAR para Determinantes

Mapa do site