Geometria III - Ângulos e Triângulos

---

ÂNGULOS

Chama-se ângulo, a figura plana limitada por duas semi-retas de mesma origem. Na figura abaixo, podemos observar que as semi-retas OA e OB determinam dois ângulos: um de abertura a (ângulo convexo) e outro de abertura b (ângulo côncavo). O ângulo convexo é indicado por BÔA e a é a medida deste ângulo.

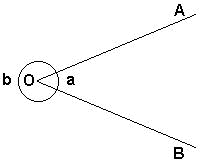
Temos: OA e OB = lados do ângulo e O = vértice do ângulo BÔA.

Medidas de ângulos
A principal unidade de medida de ângulos é o grau (símbolo º). Um ângulo raso (aquele formado por duas semiretas opostas, como o mostrado na figura abaixo), mede 180º .

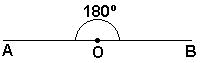
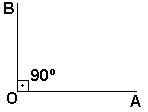
A metade de um ângulo raso, é denominado ângulo reto , e sua medida é 90° .

Concluimos que o ângulo de uma volta completa, corresponde a dois ângulos rasos ou a quatro ângulos retos e portanto sua medida é 360° .

Dividindo-se um ângulo reto em 90 partes iguais, obteremos 90 ângulos de medida 1º cada, sendo portanto 1º a unidade fundamental da medida de ângulos. Esta unidade pode também ser subdividida em unidades menores - o minuto (') e o segundo (") - de forma que: 1 grau = 60 minutos e 1 minuto = 60 segundos Simbolicamente: 1º = 60' e 1'= 60"

O uso destas subdivisões do grau, justificam-se nas medidas de ângulos nas quais se requer alto grau de precisão.

Dados os ângulos de medidas a = 30º40'32" e b = 18º53'40'', pede-se determinar os valores dos ângulos a + b e a - b.

Teremos:
a + b = 30º40'32'' + 18º53'40"
a + b = 30º + 40'+32"+18º+53'+40"
a + b =(30º+18º) + (40'+ 53') + (32"+ 40")
a + b = 48º + 93'+72"
Como 1º = 60', vem que 93'= 60'+ 33'= 1º + 33', daí, vem:
a + b = 48º + 1º + 33'+ 72"
Como 1'= 60" , vem que 72"= 60"+ 12" = 1'+ 12", vem:
a + b = 48º + 1º + 33'+ 1'+ 12"
a + b = 49º + 34'+ 12"
a + b = 49º34'12"

Vamos calcular a - b:
a - b = 30º40'32" - 18º53'40"
a - b = 30º + 40'+32"-(18º+53'+40")
a - b = (30º - 18º) + (40'- 53') + (32"- 40")
a - b = 12º + (40'- 53') + (32"- 40")
Para evitar os valores negativos nas subtrações acima, observar que:
a - b = 11º + 1º + (40'- 53') + (32"- 40")
a - b = 11º + 60'+ (40'- 53') + (32"- 40")
a - b = 11º + (100'- 53') + (32"- 40")
a - b = 11º + 47'+ (32"- 40")
a - b = 11º + 46'+ 1'+ (32"- 40")
Como 1'= 60", vem:
a - b = 11º + 46' + 60"+ (32"- 40")
a - b = 11º + 46'+ (92"- 40")
a - b = 11º + 46'+ 52"
a - b = 11º46'52"

Determine o complemento do ângulo de medida x = 56º32'40"

O complemento de um ângulo x é 90º - x. Logo, o complemento do ângulo será:
Y = 90º - x = 90º - 56º32'40" = 90º - (56º + 32' + 40") = 90º - 56º - 32' - 40"
Y = 34º - 32'- 40"
Y = 33º + 1º - 32'- 40"
Y = 33º + 60' - 32'- 40"
Y = 33º + 28'- 40"
Y = 33º + 27' + 1' - 40"
Y = 33º + 27'+ 60" - 40"
Y = 33º + 27'+ 20"
Y = 33º27'20"

Valem ainda, as seguintes definições:

• Ângulo agudo - é aquele cuja medida situa-se entre 0° e 90° .
• Ângulo obtuso - é aquele cuja medida situa-se entre 90° e 180° .
  
• Ângulos complementares - são aqueles cujas medidas somam 90° . Dizemos que cada um deles é o complemento do outro.
  Exemplo: 34° é o complemento de 56° e vice-versa , pois 34° + 56° = 90° .
  
• Ângulos suplementares - são aqueles cujas medidas somam 180° . Dizemos que cada um deles é o suplemento do outro.
  Exemplo: 48° é o suplemento de 132° e vice-versa, pois 48° + 132° = 180° .
  
• Ângulos congruentes - são aqueles que possuem medidas iguais. Assim, por exemplo todos os ângulos retos são congruentes, todos os ângulos de medida 60° são congruentes, etc.
  
• Ângulos opostos pelo vértice - como o próprio nome indica, são aqueles cujos lados de um são os prolongamentos dos lados do outro. Vale aqui, a seguinte proposição, facilmente demonstrável:
  "Dois ângulos opostos pelo vértice são congruentes, ou seja, possuem a mesma medida".
  
  
  
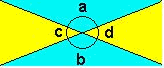
  Veja que os ângulos de medidas a e b são congruentes, e, também os ângulos de medidas c e d são também congruentes, ou seja, possuem a mesma medida.
  
  
• Retas perpendiculares - são aquelas retas concorrentes (isto é, aquelas que possuem um único ponto em comum) que formam entre si quatro ângulos retos.

  

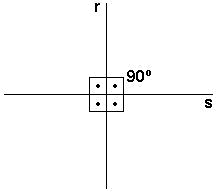
  Se duas retas r e s são perpendiculares, indicamos isso através do símbolo: r^ s.

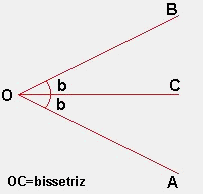
• Bissectriz de um ângulo - é a semi-reta que partindo do vértice, determina dois ângulos congruentes
  ( ou seja, de mesma medida).

Axioma: Todo ângulo, possui uma única bissectriz.

RETAS PARALELAS

Duas retas distintas r e s são paralelas, e indica-se r//s , quando estando contidas num mesmo plano (coplanares) , e não possuem ponto em comum.

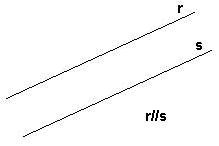
Dadas duas retas paralelas, chama-se reta transversal qualquer reta que intercepte ambas as retas. Observamos na figura, que ficam determinados oito ângulos de medidas a, b, c, d, e, f, g e h que recebem denominações especiais a saber:

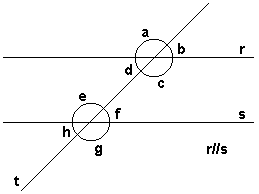
ângulos correspondentes: b e f, a e e, d e h, e c e g.
ângulos alternos internos: d e f, e c e e.
ângulos alternos externos: b e h, e a e g.
ângulos colaterais internos: d e e, e c e f.
ângulos colaterais externos: b e g, e a e h.

Observa-se que:
• os ângulos correspondentes são congruentes (medidas iguais)
• os ângulos alternos são congruentes (medidas iguais).
• os ângulos colaterais são suplementares, isto é, somam 180° .

TRIÂNGULOS

Dados 3 pontos A , B e C , não colineares, isto é , não alinhados , chama-se Triângulo à região do plano limitada pelos segmentos AB , AC e BC , denominados lados , sendo A , B e C os seus vértices. Os ângulos internos são representados por Ð A , Ð B e Ð C , ou simplesmente A , B e C.

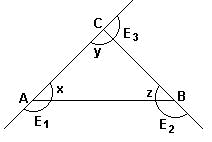
Na figura acima, teremos então:

• Soma dos ângulos internos: x + y + z = 180º
• Soma do ângulos externos: E₁ + E₂ + E₃ = 360º
• Em todo triângulo, um ângulo externo é igual à soma dos ângulos internos não adjacentes, ou seja:
  E₁ = y + z
  E₂ = x + y
  E₃ = x + z

Vamos provar as três propriedades acima:

A primeira é imediata, a partir da observação atenta da figura abaixo, se lembrarmos que os ângulos alternos internos possuem a mesma medida. Assim, x = m e y = n. E como sabemos que z + m + n = 180º, vem finalmente: x + y + z = 180º.

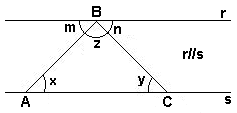
Para provar a segunda, basta observar que x + E₁ = z + E₂ = y + E₃ = 180º.
Logo, podemos escrever: (x + E₁ ) + ( z + E₂ ) + ( y + E₃ ) = 180º + 180º + 180º
Arrumando convenientemente, vem:
x + y + z + E₁ + E₂ + E₃ = 540º
E como x + y + z = 180º , substituindo, vem:
180º + E₁ + E₂ + E₃ = 540º
De onde finalmente tiramos: E₁ + E₂ + E₃ = 360º
Para provar a terceira, observe que podemos escrever:
x + y + z = 180º = x + E₁, de onde tiramos: E₁ = y + z. Os outros casos, são análogos.

Outra propriedade importante dos triângulos é que a medida de qualquer lado é menor que a soma das medidas dos outros dois.
Sendo a , b e c as medidas dos lados de um triângulo qualquer, teremos sempre:
a < b + c
b < a + c
c < a + b
conhecidas como Desigualdades Triangulares.

DICA: se um triângulo possui dois lados medindo a e b, o terceiro lado estará compreendido entre
|a - b| e (a + b).
Assim, por exemplo, se um triângulo possui dois lados de medidas 10 e 30, o terceiro lado estará compreendido entre 30-10 e 30+10, ou seja, entre 20 e 40.

Os triângulos podem ser classificados quanto à medida dos lados em:

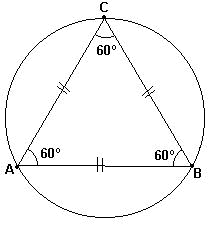
EQUILÁTEROS: medidas dos lados iguais; como consequencia disto , os 3 ângulos internos de um triângulo equilátero são congruentes, isto é , possuem a mesma medida e, portanto cada ângulo mede 60° .

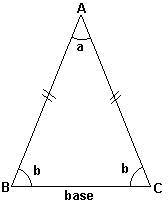
ISÓSCELES: possuem dois lados com medidas iguais. O terceiro lado chama-se base.Verifica-se facilmente, que os ângulos da base de um triângulo isósceles possuem medidas iguais, ou seja, são congruentes.

ESCALENO: possui os tres lados desiguais.

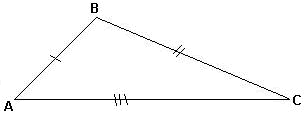
Infere-se , portanto, que todo triângulo equilátero é isósceles, o que significa que o conjunto de todos os triângulos equiláteros é um subconjunto do conjunto de todos os triângulos isósceles.

Os triângulos podem ser classificados quanto às medidas dos ângulos internos , em:

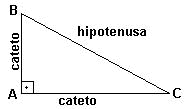
RETÂNGULO: possuem um ângulo reto ( 90° ). O lado oposto ao ângulo reto é chamado hipotenusa e os outros 2 lados, são chamados catetos.

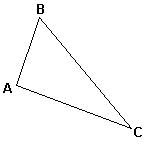
ACUTÂNGULO: todos os ângulos são agudos.

OBTUSÂNGULO: possui um ângulo obtuso.

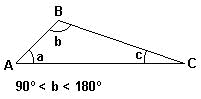
Elementos lineares de um triângulo.

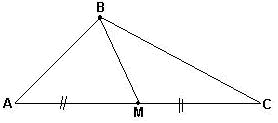
Mediana - é o segmento que une um vértice ao ponto médio do lado oposto. Conclui-se que todo triângulo possui 3 medianas; o ponto de interseção das 3 medianas de um triângulo, encontram-se em um ponto denominado BARICENTRO ou CENTRO DE GRAVIDADE do triângulo.

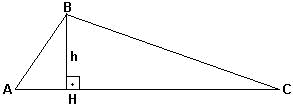
Altura - é o segmento que une um vértice ao lado oposto (ou ao prolongamento deste), sendo perpendicular a esse lado. As 3 alturas de um triângulo passam por um mesmo ponto, chamado ORTOCENTRO do triângulo.

Bissectriz interna - é o segmento que divide cada ângulo interno do triângulo, em 2 ângulos iguais. As 3 bissectrizes internas de um triângulo passam por um ponto chamado INCENTRO do triângulo. O incentro é o centro da circunferência inscrita no triângulo, isto é , da circunferência que tangencia os 3 lados do triângulo.

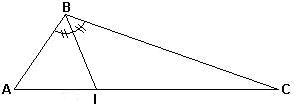
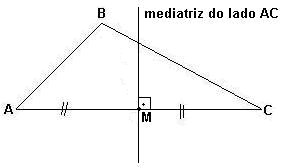
Mediatriz - é a reta perpendicular ao lado, passando pelo ponto médio do mesmo. As 3 mediatrizes de qualquer triângulo passam por um mesmo ponto, chamado CIRCUNCENTRO, que é o centro da circunferência circunscrita ao triângulo, isto é , da circunferência que passa pelos 3 vértices do triângulo.

TEOREMA DE TALES

Um feixe de paralelas determina sobre duas retas transversais quaisquer, segmentos proporcionais.
Assim, na figura abaixo, o teorema de Tales nos permite escrever:

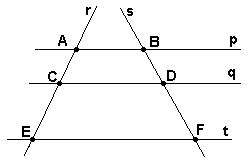
O teorema de Tales ( matemático grego, do século VI a.C.) é um dos mais importantes da Geometria, pois, dele, se deduzem como consequências, outros teoremas importantes, como os casos de semelhança de triângulos, o teorema de Pitágoras, etc, temas que serão abordados em breve.

Para encerrar por hoje, vamos resolver a questão a seguir: Na figura abaixo, temos BG//CF//DE. Pede-se calcular o valor de a, b e c, sabendo-se que a soma a + b + c = 45.

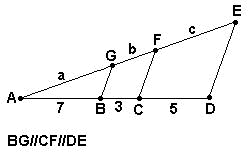
Pelo Teorema de Tales, podemos escrever:

Usando uma propriedade das proporções, podemos escrever também:

Portanto, a = 21, b = 9 e c = 15.

Paulo Marques, 31/10/1999 - Feira de Santana - BA.

---

VOLTAR