Geometria VI - Volume de pirâmide I

Calcule o volume da pirâmide PQRS mostrada na figura abaixo.

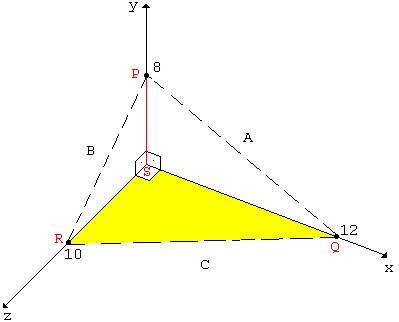
Solução:

O volume de uma pirâmide é calculado pela fórmula 
V = (1/3).S_b.h, onde S_b é a área da base e h a sua altura (da pirâmide, é claro!). 

Olhando simplesmente a figura, concluímos que a altura da pirâmide é igual a h = SP = 8.  
A base da pirâmide é um triângulo retângulo de lados SR = 10 e  SQ = 12. Portanto, a área da base vale:
S_b = (1/2).b.h = (1/2).SR.SQ = (1/2).10.12 = 60

Lembrando que a altura da pirâmide mede h = SP = 8, fica:
O  volume procurado ser igual a:   V = (1/3).60.8 = 160 u.v.  
Nota: u.v = unidade de volume

Se as distâncias fossem dadas em cm, a resposta seria em cm³. Se em m, m³, ..., etc. Aí, você entende melhor o significado de u.v. OK?

Agora resolva este:

Calcule o volume da pirâmide PQRS mostrada na figura abaixo:

Atenção: este tem um pouco mais de dificuldade que o exercício resolvido acima; veja a solução no arquivo  Volume de Pirâmide II.
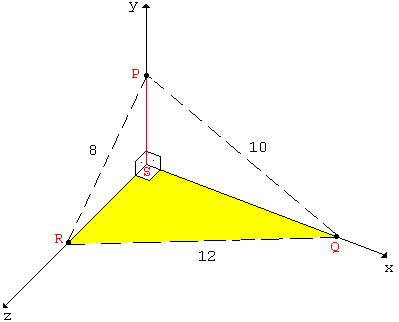
Paulo Marques, 25 de dezembro de 2000; revisado e ampliado em 16/12/2008.
VOLTAR