| Num poste de iluminação pública, uma lâmpada incandescente ainda do século XX. |
Nota: a resolução desta questão requer noções de derivadas
Uma lâmpada de um poste de iluminação pública está situada a uma altura de 6m. Se uma pessoa de 1,80m de altura, posicionada embaixo da lâmpada, caminhar afastando-se da lâmpada a uma velocidade de 5m/s, com qual velocidade se desloca a extremidade de sua sombra projetada na rua?
SOLUÇÃO:
Considere a figura a seguir:
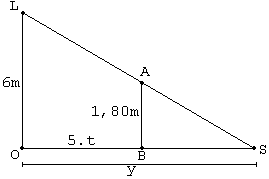
Supondo que a pessoa partiu do ponto O a uma velocidade de 5m/s, depois de t segundos, ela terá percorrido a distância d = 5.t e estará no ponto B.
Como a luz se propaga em linha reta, a ponta da sombra da pessoa, estará no ponto S. Seja y esta distância.
Pela semelhança dos triângulos BAS e OLS, poderemos escrever:
![]()
Substituindo os valores, vem:
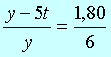
Daí, fica:
6(y –
5t) = 1,80.y
6y –
30t = 1,80y
6y –
1,80y = 30t
4,20y =
30t
y =
(30/4,20)t
y =
7,14t
Ora, a velocidade v do ponto S será a derivada dy/dt, ou seja:
Como y
= 7,14t, vem imediatamente que:
![]()
Portanto, a velocidade do ponto extremo da sombra é igual a
7,14 m/s.
Agora, um problema bem simples cuja solução não
necessita do uso do conceito de derivada, mas, que no fundo, tem tudo a ver, pois envolve o conceito de velocidade e, como vimos,
a velocidade v é a derivada do espaço (y) em relação ao
tempo (t) ou seja:
v = dy / dt . Neste caso, poderemos
escrever dy = v . dt . Esta igualdade é uma forma bem simples de introduzir o
conceito da operação inversa da derivada, que é
a integral. Voltaremos a este assunto em breve.
Eis a questão:
Uma pessoa acende uma lanterna no instante t = 0. Após um milésimo de segundo, qual a distância
y alcançada pela luz da lanterna?
Solução: sabemos que a velocidade da luz é igual a 300000 km/s. Logo,
y = vt, onde t = 1/1000 s. Logo,
y = 300000 km/s . (1/1000) s = 300000/1000 = 300 km. Simples, assim.
Nota: a fórmula y = v.t é apenas um caso
particular da expressão geral dy = v.dt , a qual será analisada em breve,
conforme dissemos acima.