| Uma secretária muito distraída |
FUVEST 2000 - 1ª FASE - Um
arquivo de escritório possui 4 gavetas, chamadas a , b , c
, d.
Em cada gaveta cabem no máximo 5 pastas. Uma secretária guardou,
ao acaso, 18 pastas nesse arquivo. Qual é a probabilidade de haver exatamente 4
pastas na gaveta a ?
a) 3/10
b)
1/10
c)
3/20
d)
1/20
e)
1/30
Solução:
Sejam x, y, z, w, as quantidades de pastas em cada gaveta. Necessariamente deveremos ter x + y + z + w = 18, que é o número de pastas que a secretária distraída guardou.
Esta equação
linear, com a condição
de no máximo 5 pastas por gaveta, conforme enunciado, somente é verificada
para as seguintes condições:
5 + 5 + 5 + 3 = 18 OU
5 + 5 + 4 + 4 = 18
Trata-se então, de um problema de
permutações com elementos repetidos.
O número total de possibilidades
para a primeira condição, será dada por:
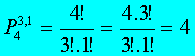
O número total de possibilidades para a segunda condição será dada,
analogamente por:
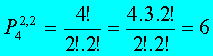
Como pode ocorrer uma situação OU outra, o número total de possibilidades será igual à soma: 4 + 6 = 10 possibilidades.
Este número, representa o total
de possibilidades, sendo portanto, o número de elementos do espaço amostral U,
ou seja:
n(U) = 10.
Para calcular a probabilidade solicitada, deveremos saber antes, o número de eventos favoráveis – n(E) - que satisfaçam a condição especificada no problema, ou seja: haver exatamente 4 pastas na gaveta a.
O número de eventos favoráveis
deverá portanto obedecer a condição:
4 + (5 + 5 + 4)
Como o 4 na primeira gaveta é fixo, teremos que calcular o número de permutações dos 3 elementos restantes, com 2 elementos repetidos, ou seja:
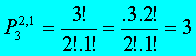
Ora, temos 3 eventos favoráveis, num total de
10 possibilidades, ou seja: n(U) =
10 e n(E) = 3.
Logo, a probabilidade
procurada será, finalmente, igual a:
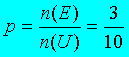
Que é a resposta do problema, ou seja, alternativa A.
Também podemos exprimir o
resultado acima na forma percentual, ou seja:
3/10 = 0,30 = 30/100 = 30%
Assuntos
que devem ser revisados:
Análise
Combinatória
Probabilidades
Paulo Marques - Feira de Santana - BA - 01 outubro de 2000.