Exercícios Resolvidos de Trigonometria

1 - (UNI-RIO) Os lados de um triângulo são 3, 4 e 6. O cosseno do maior ângulo interno desse triângulo vale:

a) 11 / 24
b) - 11 / 24
c) 3 / 8
d) - 3 / 8
e) - 3 / 10

Solução:
 
Sabemos que num triângulo, ao maior lado opõe-se o maior ângulo. Logo, o maior ângulo será aquele oposto ao lado de medida 6. Teremos então, aplicando a lei dos cossenos:

6² = 3² + 4² - 2 . 3 . 4 . cos b \ 36 - 9 - 16 = - 24 . cos b \ cos b = - 11 / 24 e, portanto, a alternativa correta é a letra B.

Lembrete: TC - Teorema dos cossenos: Em todo triângulo, o quadrado de um lado é igual à soma dos quadrados dos outros dois, menos o dobro do produto desses lados pelo cosseno do angulo que eles formam.

2 - (UNESP) Se x e y são dois arcos complementares, então podemos afirmar que
A = (cosx - cosy)² + (senx + seny)² é igual a:

a) 0
b) 1/2
c) 3/2
d) 1
e) 2

Solução:
 
Desenvolvendo os quadrados, vem:
A = cos² x - 2 . cosx . cosy + cos² y + sen² x + 2 . senx . seny + sen² y
Organizando convenientemente a expressão, vem:
A = (cos² x + sen² x) + (sen² y + cos² y) - 2 . cosx . cosy + 2 . senx . seny
A = 1 + 1 - 2 . cosx . cosy + 2 . senx . seny
A = 2 - 2 . cosx . cosy + 2 . senx . seny
Como os arcos são complementares, isto significa que x + y = 90º \ y = 90º - x.
Substituindo, vem:
A = 2 - 2 . cosx . cos(90º - x) + 2 . senx . sen(90º - x)
Mas, cos(90º - x) = senx e sen(90º - x) = cosx, pois sabemos que o seno de um arco é igual ao cosseno do seu complemento e o cosseno de um arco é igual ao seno do seu complemento.
Logo, substituindo, fica:
A = 2 - 2 . cosx . senx + 2 . senx . cosx
A = 2 + (2senxcosx - 2senxcosx) = 2 + 0 = 2 , e portanto a alternativa correta é
a letra E.

3 - Calcule sen 2x sabendo-se que tg x + cotg x = 3.

Solução:
 
Escrevendo a tgx e cotgx em função de senx e cosx , vem:

Daí, vem: 1 = 3 . senx . cosx \ senx . cosx = 1 / 3. Ora, sabemos que
sen 2x = 2 . senx . cosx e portanto senx . cosx = (sen 2x) / 2 , que substituindo vem:
(sen 2x) / 2 = 1 / 3 e, portanto, sen 2x = 2 / 3.
Resposta: 2 / 3

4 - (ITA - 96) Seja a Î [0, p /2], tal que sen a + cos a = m .
Então, o valor de

é:

a) 2(m² - 1) / m(4 - m²)
b) 2(m² + 1) / m(4 + m²)
c) 2(m² - 1) / m(3 - m²)
d) 2(m² - 1) / m(3 + m²)
e) 2(m² + 1) / (3 - m²)

Solução:

Quadrando ambos os membros da expressão dada, vem:
(sen a + cos a )² = m² . Desenvolvendo, fica:
sen² a + 2 . sen a . cos a + cos² a = m²
Simplificando, vem: 1 + 2 . sen a . cos a = m² \ 1 + sen 2a = m² e, portanto,
sen 2a = m² - 1
Seguindo o mesmo raciocínio, vamos elevar ambos os membros da expressão dada ao cubo:
Lembrete: (a + b)³ = a³ + b³ + 3(a +b) . ab
Logo:
(sen a + cos a )³ = m³ . Desenvolvendo, vem:
sen³ a + cos³ a + 3 (sen a + cos a ) (sen a . cos a ) = m³
Lembrando que sen a + cos a = m e sen a . cos a = sen 2a / 2, e substituindo, fica:
sen³ a + cos³ a = m³ - 3 (m) . (m² - 1) / 2
Substituindo esses valores encontrados na expressão dada, teremos então:

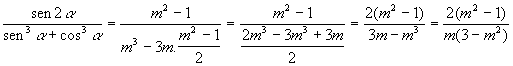
E portanto, a alternativa correta é a letra C.

Paulo Marques - Feira de Santana - BA, nos idos de outubro 1997, com revisão em 30/09/06.

CONTINUAR              VOLTAR