| Trigonometria II |
Funções trigonométricas: seno, cosseno , tangente, cotangente, secante e cossecante.
Considere a figura abaixo, onde está
representado um círculo trigonométrico (centro na origem e
raio unitário).
Da simples observação da figura, temos os
seguintes pontos notáveis:
A(1;0) , B(0;1) , A’(-1;0) e B’(0;-1).
Definiremos os seguintes eixos:
A’A = eixo dos cossenos (variando no intervalo real de -1 a
+1)
B’B = eixo dos senos (variando no intervalo real de -1 a +1)
AT = eixo das tangentes ® variando no intervalo real (-¥ , +¥ ).
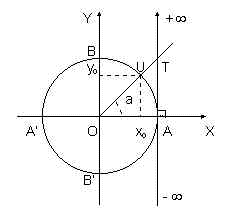
Observe também que as coordenadas
cartesianas do ponto U são:
x0 = abscissa e y0 = ordenada, ou seja: U(x0
, y0).
Considere o arco trigonométrico AU de medida a.
Nestas condições definimos:
1 - Seno do arco de medida a = ordenada do ponto U
= y0 e indicamos: sen a = y0
.
2 - Cosseno do arco de medida a = abscissa do ponto U
= x0 e indicamos: cos a = x0
Lembrando que o raio do círculo trigonométrico
é igual a 1 (por definição), concluímos que o seno e o cosseno de um arco são números reais que variam no
intervalo real de -1 a +1.
Da figura acima, podemos escrever: x02 + y02
= OU2; mas, OU = raio do círculo trigonométrico
e
portanto vale 1.
Daí vem a seguinte relação entre o seno e o
cosseno de um arco, já que x0 = cos a e y0
= sen a :
sen2a
+ cos2a = 1 ,
denominada relação fundamental da
Trigonometria.
Observando ainda a figura acima e
considerando os sinais das ordenadas e das abscissa ou seja,
sinais do seno e do cosseno, podemos concluir que o seno é
positivo para os arcos compreendidos entre 0º e 180º (1º e 2º
quadrantes) e negativo para os arcos compreendidos entre 180º e
360º (3º e 4º quadrantes).
Já para o cosseno, usando a mesma consideração anterior,
concluímos que o cosseno é positivo para os arcos compreendidos
entre 0º e 90º (1º quadrante) e para os arcos compreendidos
entre 270º e 360º (4º quadrante) e, negativo para os arcos
compreendidos entre 90º e 180º (2º quadrante) e para os arcos
compreendidos entre 180º e 270º (3º quadrante).
Valores notáveis do seno e cosseno:
sen 0º = sen 180º = cos 90º = cos 270º = 0
sen 90º = cos 0º = cos 360º = 1
sen 270º = cos 180º = -1
Ainda na figura anterior, observe o segmento AT.
O comprimento deste segmento, é por definição,
a tangente do arco AU de medida a.
Indicamos isto escrevendo tg a
= AT.
A escala adotada no eixo das tangentes é a mesma dos eixos
das abscissa e das ordenadas.
Pela semelhança dos triângulos Ox0U
e OAT, podemos escrever:
![]() ;
;
mas como y0 = sen a, x0 = cos a, AT = tg a
e OA = 1, vem:
![]()
para cos a ¹
0.
Nota: para saber o sinal da tangente nos 4
quadrantes, basta usar a regra de sinais da divisão, já que a
tangente é simplesmente o quociente do seno pelo cosseno, cujos
sinais nos quadrantes já conhecemos.
Somente como exemplo, como
o seno e o cosseno são negativos no 3º quadrante, sendo a
tangente o quociente entre eles, concluímos que neste quadrante,
a tangente será positiva, pois menos dividido por menos dá
mais!
Os inversos multiplicativos do seno, cosseno e tangente, recebem designações particulares a saber:
1 - inverso do seno = cossecante (símbolo:
cossec)
2 - inverso do cosseno = secante (símbolo: sec)
3 - inverso da tangente = cotangente (símbolo: cotg )
Assim, sendo a um arco trigonométrico, poderemos escrever:
![]()
para sen a ¹
0.
![]()
para cos a ¹
0.
![]()
para sen a ¹
0.
Exercícios Resolvidos
1. Qual o valor máximo da função y = 10
+ 5 cos 20x ?
Solução:
O
valor máximo da função ocorre quando o fator cos20x é máximo,
isto é, quando cos 20x = 1. Logo, o valor máximo da função
será y = 10 + 5.1 = 15.
2. Qual o valor mínimo da função y = 3 +
5 sen 2x?
Solução:
O
valor mínimo da função ocorre quando o fator sen2x é mínimo,
isto é, quando sen2x = -1.
Logo, o valor mínimo da função será
y = 3 + 5(-1) = - 2 .
3. Qual o valor máximo da função ![]() ?
?
Solução:
A função terá valor máximo,
quando o denominador tiver valor mínimo. Para que o denominador
seja mínimo, deveremos ter cos 20x = 1 \
y = 10 / (6 - 2.1) = 10 / 4 = 5/2.
Portanto, o valor máximo da função é 5/2.
Qual seria o valor mínimo da mesma função?
Resposta: 5/4
4. Para que valores de m a equação sen 30x
= m - 1 tem solução?
Solução:
Ora, o seno de qualquer
arco, é sempre um número real pertencente ao intervalo fechado
[-1,1]. Logo, deveremos ter: -1 £ m -1 £ 1 \ 0 £ m £ 2.
Agora calcule:
a) o valor mínimo da função y = 2 + 9sen4x.
b) o valor máximo da função y = 10 - cosx .
c) o valor de y = sen 180º - cos270º
d) o valor de y = cos 180º - sen 270º
e) o valor de y = cos(360.k) + sen(360.k), para k inteiro.
Respostas: a) - 7 b) 11 c) 0 d) 0 e) 1
Paulo Marques - Feira de Santana - BA, nos idos de 1997, com revisão em 30/09/06.
CONTINUAR
VOLTAR