| Trigonometria IV |
1 - Simplifique a expressão a seguir:
![]()
Solução:
Das aulas anteriores, poderemos escrever:
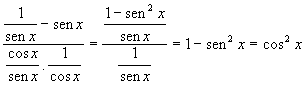
2 - Sendo x um arco tal que cosx = tgx , calcule senx.
Solução:
Sabemos
que tgx = senx / cosx.
Substituindo tgx por cosx (dado do
problema), vem:
cosx = senx / cosx donde vem: cos2x = senx. Mas,
cos2x = 1 - sen2x .
Substituindo, fica: 1 -
sen2x = senx.
Daí, vem: sen2x + senx - 1 = 0
Fazendo senx = y e substituindo: y2 + y - 1 = 0.
Resolvendo esta equação do 2º grau, usando a fórmula de
Bhaskara, fica:
![]()
Como y = senx, somos tentados a dizer que
existem dois valores para senx, dados pela igualdade acima.
Lembre-se porém que o seno de um arco é um número que pode
variar
de -1 a +1. Portanto, somente um dos valores acima
satisfaz o problema ou seja:
![]() que é a resposta procurada.
que é a resposta procurada.
3
- Para que valor de m a expressão
y = (m - 1)(sen4x - cos4x) + 2cos2x
+ m.cosx - 2.cosx + 1 é independente de x?
Solução:
Podemos escrever:
y = (m - 1)[(sen2x - cos2x)(sen2x
+ cos2x)] + 2cos2x + mcosx - 2cosx + 1
Como sen2x + cos2x = 1, substituindo, fica:
y = (m - 1)(sen2x - cos2x) + 2cos2x
+ mcosx - 2cosx + 1
y = msen2x - mcos2x - sen2x +
cos2x + 2cos2x + mcosx - 2cosx + 1
Escrevendo tudo em função de cosx, lembrando que sen2x
= 1 - cos2x, vem:
y = m(1 - cos2x) - mcos2x - (1 - cos2x)
+ cos2x + 2cos2x + mcosx - 2cosx + 1
y = m - mcos2x - mcos2x - 1 + cos2x
+ cos2x + 2cos2x + mcosx - 2cosx + 1
Simplificando os termos semelhantes, fica:
y = m + (4 - 2m)cos2x + (m - 2)cosx
Para que a expressão acima seja independente de x,
deveremos ter necessariamente 4 - 2m = 0 e m - 2 = 0
\ m = 2, que
é a resposta procurada.
4
- Agora resolva você mesmo:
Para que valor de m a expressão
y = m(sen4x - cos4x) + 2cos2x -
1 + m é independente de x?
Resposta: m = 1
5
- Sabendo que senx + cosx = m, calcule (m2 - 1)y
sendo
y dado pela expressão:
![]()
Resposta: m(3 - m2).
Sugestão: Eleve ambos os membros da igualdade dada ao cubo, ou
seja:
(senx + cosx)3 = m3 , lembrando que (a+b)3
= a3 + b3 + 3(a+b).ab.
Eleve também ambos os membros da expressão dada ao quadrado, ou
seja:
(senx + cosx)2 = m2 , lembrando que (a+b)2
= a2 + 2ab + b2.
Paulo Marques - Feira de Santana - BA, nos idos de setembro 1997, com revisão em 30/09/06.
CONTINUAR
VOLTAR