Fórmula de Moivre (Abraham De Moivre - matemático francês - 1667 - 1754)

Exemplos:
(cos 30º + i . sen 30º)² = cos 60º + i . sen 60º (onde  n = 2)
(cos 30º + i . sen 30º)³ = cos 90º + i . sen 90º = 0 + i . 1 = i (onde: n = 3)

Exercício resolvido: Calcule:

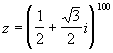
Solução: Observe que 1 / 2 = cos 60º e Ö 3 /2 = sen 60º . Logo, podemos escrever:
z = (cos 60º + i . sen 60º)¹⁰⁰ = cos (60 . 100) + i . sen (60 . 100) , de acordo com a fórmula de Moivre. Logo:
z = cos 6000º + i . sen 6000º . Como o argumento do complexo é 6000º , um arco maior que uma volta, devemos dividi-lo por 360º para retirar as voltas completas e considerar o resto da divisão. O resto da divisão de 6000º por
360º é 240º . Logo, z = cos 240º + i . sen 240º = - 1 /2 - Ö 3 / 2 i , pois
cos 240º = - 1 / 2 e sen 240º = - Ö 3 / 2 . Assim, a resposta do problema é:

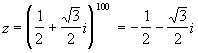
Aplicações diretas da fórmula de Moivre 
a) Fórmulas do arco duplo
Fazendo n = 2 na fórmula de Moivre, vem:
(cos q + i . sen q ) ² = cos 2 q + i . sen 2 q
Desenvolvendo o primeiro membro da expressão acima e igualando, vem:

Como i² = -1, vem:

Comparando as igualdades, teremos finalmente:
(cosseno do arco duplo)
sen2q = 2 senq cosq (seno do arco duplo)

b) Fórmulas do arco triplo
Fazendo n = 3 na fórmula de Moivre, obteremos: (Tente como exercício).
(cosseno do arco triplo)
(seno do arco triplo)
Nota: Lembre-se que (x+y)³ = x³ + 3.x².y + 3.x.y² + y³ e faça n = 3 na fórmula de Moivre.

Paulo Marques - Feira de Santana - BA - 25 de setembro de 1999

VOLTAR