| Módulo III - Inequações Modulares |
1 - Introdução
Já sabemos que o módulo de um número
real é um número positivo ou nulo, o que nos leva a
interpretar que o módulo de um número real está
diretamente associado à noção de distância.
Assim, dado um número real x, o módulo de x - representado por
|x| - é igual geometricamente, à distancia à origem O, do
ponto P, representativo do número x na reta real - também
conhecida como reta numerada.
Consideremos por exemplo a reta numerada a
seguir:
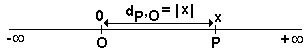
Teremos: |x| = distancia de P a O = dP,O
Vamos utilizar a interpretação geométrica do módulo vista
acima, para resolver as desigualdades ou inequações modulares.
Inequações do tipo |y| £ b, com b > 0.
Resolver a inequação acima, significa
determinar quais os números reais cuja distancia à origem O, são
menores ou iguais ao número positivo b.
Da figura abaixo, infere-se imediatamente que os números
procurados estão situados no intervalo fechado [-b, b].
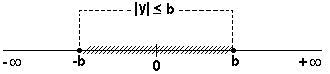
Assim, podemos escrever a seguinte regra
geral:
|y| £ b Û - b £ y £ b, para b real e positivo.
Inequações do tipo |y| ³ b, com b > 0.
Resolver a inequação acima, significa
determinar quais os números reais cuja distancia à origem O, são
maiores ou iguais ao número positivo b.
Utilizando o mesmo raciocínio anterior, concluímos
imediatamente que os números procurados estão situados nos
intervalos (-¥ , - b] ou [b, +¥ ).
Assim, podemos escrever a seguinte regra geral:
|y| ³ b Û y ³ b ou y £ - b, para b real e
positivo.
Veja a figura abaixo, a qual lhe ajudará no entendimento da importante propriedade vista acima.
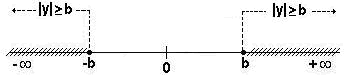
2 - Exercícios resolvidos
Resolva em R - conjunto dos números
reais - as seguintes inequações modulares:
a) |2x + 5| £ 11
SOLUÇÃO:
Vem imediatamente que: -11 £ 2x + 5 £ 11
Somando -5 a todos os membros, fica: -16 £ 2x £ 6
Daí, então, dividindo tudo por 2, concluímos finalmente: -8 £ x £ 3.
Logo, o conjunto solução da inequação dada será o conjunto S
dado por:
S = {x Î R;
-8 £ x £ 3} , que, representado
na forma de um intervalo real, seria indicado por S = [-8, 3].
Graficamente, teríamos:
![]()
Observe que no conjunto R dos números
reais, o conjunto solução da inequação dada é um conjunto
infinito formado por todos os números reais a partir de - 8
até +3.
Se, por exemplo, fosse pedido o conjunto solução da mesma
inequação no conjunto Z dos números inteiros, o conjunto solução
seria FINITO, e igual a:
S = {-8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3}.
Se, por exemplo, fosse pedido o conjunto solução da mesma
inequação no conjunto N dos números naturais, o conjunto solução
seria FINITO, e igual a:
S = {0, 1, 2, 3}.
É muito importante estar atento ao
conjunto universo adotado na questão proposta.
Caso não seja feita nenhuma referencia, deveremos
considerar que o conjunto universo adotado é sempre R - conjunto
dos números reais.
b)
|x - 1| > 5
SOLUÇÃO:
Teremos: x - 1 > 5 OU x - 1 < - 5
Portanto, x > 6 OU x < - 4.
O conjunto solução em R, será então: S = {x Î R; x > 6 ou x < - 4} .
Na forma de intervalo, teremos: S = (-¥ , -4) È (6, ¥ ).
Graficamente, teríamos:
![]()
Observe que, utilizando o conceito de
diferença de conjuntos, poderemos exprimir o conjunto solução
S também na forma:
S = R - [-4, 6], onde R é o conjunto dos números
reais.
c)
|x + 3| + |2x - 8|
³ 20
SOLUÇÃO:
Como não podemos somar diretamente os módulos, vamos considerar
o que segue:
Observe que as expressões entre módulo, se anulam para x = -3 e
x = 4.
Temos tres casos a considerar:
1º caso: x < -3
Neste caso, teremos:
x + 3 < 0
Þ |x + 3| =
- (x + 3)
2x - 8 <
0 Þ |2x - 8|
= - (2x - 8)
Assim, a inequação dada será equivalente a:
- (x + 3) - (2x - 8) ³ 20 ou, eliminando os parênteses:
- x - 3 - 2x + 8 ³ 20
Portanto, teremos que determinar os valores de x que satisfaçam
à dupla desigualdade:
x < - 3 e - x - 3 - 2x + 8 ³ 20.
Resolvendo este sistema de inequações,
vem:
x < - 3 e x £ - 5, que é equivalente a x £ - 5.
Então, a primeira parte da solução
do problema é o conjunto
S1 = {x Î R; x £ - 5} = ( - ¥ , -5].
2º caso: - 3 £ x < 4
Neste caso, teremos:
x + 3 > 0
Þ |x + 3| =
x + 3
2x - 8 <
0 Þ |2x - 8|
= - (2x - 8)
Assim, a inequação dada será equivalente a:
x + 3 - (2x - 8) ³ 20
Portanto, teremos que determinar os valores de x que satisfaçam
à dupla desigualdade:
- 3 £ x < 4 e x + 3 -
(2x - 8) ³
20
Resolvendo este sistema de inequações, vem:
- 3 £ x < 4 e x £ - 9
Percebemos da figura abaixo, que a interseção é vazia,
portanto, S2 = Æ .
3º caso: x ³ 4
Neste caso, teremos:
x + 3 > 0
Þ |x + 3| =
x + 3
2x - 8 >
0 Þ |2x - 8|
= 2x - 8
Assim, a inequação dada será equivalente a:
x + 3 + 2x - 8 ³ 20
Portanto, teremos que determinar os valores de x que satisfaçam
à dupla desigualdade:
x ³ 4 e x + 3 + 2x - 8 ³ 20
Resolvendo este sistema de inequações,
vem:
x ³ 4 e x ³ 25/3, que é
equivalente a x ³ 25/3, conforme podemos observar na figura abaixo.
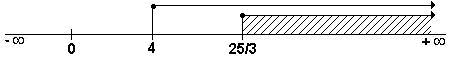
Portanto, a terceira solução parcial
será: S3 = {x Î R; x ³ 25/3} = [25/3, ¥ )
A solução geral da inequação dada será então:
S = S1 È S2 È S3 = ( - ¥ , -5] È Æ È [25/3, ¥ ) = ( - ¥ , -5] È [25/3, ¥ )
S = ( - ¥ , -5] È [25/3, ¥ ).
![]()
SOLUÇÃO:
Observando que x2 - 10x + 25 = (x - 5)2 e
lembrando que Ö a2 = |a|, vem:
Para revisar módulo, CLIQUE AQUI. Para retornar,
clique em VOLTAR no seu browser.
Portanto, |x - 5| £ ![]() 1 Û -1 £ x - 5 £ 1 Û -1 + 5 £ x - 5 + 5 £ 1 + 5 Û 4 £ x £ 6.
1 Û -1 £ x - 5 £ 1 Û -1 + 5 £ x - 5 + 5 £ 1 + 5 Û 4 £ x £ 6.
Logo, o conjunto solução da inequação dada, será o intervalo
real:
S = [4, 6].
|3x - 9| £ 2x
SOLUÇÃO:
Observe que a expressão entre módulo, se anula para x = 3.
Teremos então dois casos a considerar:
1º caso: x < 3 Þ 3x - 9 < 0 Þ |3x - 9| = -(3x - 9) = - 3x + 9
Portanto, a inequação fica: -3x + 9 £ 2x
Teremos então de resolver a dupla desigualdade:
x < 3 e -3x
+ 9 £ 2x
Vem, x <
3 e 9 £ 5x Û x < 3 e 9 /5£ x Û 9 /5£ x < 3
Portanto, para o primeiro caso, teremos o conjunto solução
parcial
S1 = [9/5, 3)
2º caso: x ³ 3 Þ 3x - 9 ³ 0 Þ |3x - 9| = 3x - 9
Portanto, a inequação fica: 3x - 9 £ 2x
Teremos então de resolver a dupla desigualdade:
x ³ 3 e 3x
- 9 £ 2x
Vem, x ³ 3
e - 9 £ - x
Û 3 £ x e 9 ³ x Û 3 £ x e x £ 9 Û 3 £ x £ 9
Portanto, para o segundo caso, teremos o conjunto solução
parcial
S2 = [3, 9]
A solução geral da inequação proposta será então:
S = S1 È S2 = [9/5, 3) È [3, 9] = [9/5, 9].
S = [9/5, 9].
Graficamente, teríamos na reta real:

Agora, resolva esta:
|x - 3| + |x| +
|x + 3| £ 9
Resposta: S = {x Î R; -3 £ x £ 3} = [-3, 3].
Paulo Marques, Feira de Santana - BA, 02/12/1999.