|
No reino da bicharada e outros problemas |
1No livro “Elementos de
Álgebra, publicado em 1770, o matemático suiço
Leonhard Euler, 1707 - 1783 – propôs o seguinte problema:
Uma lebre está 50 pulos à frente de um cachorro, o
qual dá 3 pulos no tempo que ela leva para dar 4. Sabendo que
2 pulos do cachorro valem 3 da lebre, quantos pulos ele deve dar
para pegá-la?
Solução:
Acompanhem o seguinte raciocínio
simples:
Se 2
pulos do cachorro equivalem a 3
pulos da lebre então é óbvio que 1
pulo do cachorro será equivalente a 1,5
pulos da lebre.
Logo, 3
pulos do cachorro será equivalente a 3 x 1,5 = 4,5
pulos da lebre.
Então, a cada seq��ncia de 3 pulos do
cachorro, ele se aproxima 4,5 – 4 = 0,5 pulo (da lebre).
Como
a distancia inicial entre eles é igual a 50 pulos (da lebre),
o cachorro para vencer a distância deverá dar 50 / 0,5 =
100 seqüências de 3
pulos(do cachorro), ou seja 100 x 3 = 300 pulos.
Resposta:
o cachorro deverá dar 300 pulos.
2
Um rato sai correndo e quando deu 200 pulos o
gato parte ao seu encalço. Enquanto o gato dá 3 pulos, o
rato dá 11 pulos, porém 2 pulos do gato valem 9 do
rato. Quantos pulos o gato deverá dar para alcançar o
rato?
Solução:
Acompanhem
o seguinte raciocínio simples, similar ao anterior:
2
pulos do gato = 9 pulos do rato. Daí, é claro que:
1
pulo do gato = 4,5 pulos do rato e,
3 pulos do gato = 3 x 4,5 =
13,5 pulos do rato
Em cada seqüência
de 3 pulos, o gato se aproxima 13,5 – 11 = 2,5 pulos (do
rato).
Como a distancia entre eles é de 200 pulos (do
rato), o gato, para vencer a distancia, deverá dar 200/2,5 =
80 seqüências de 3 pulos,
ou seja: 80 x 3 = 240
pulos.
Resposta: o gato deverá
dar 240 pulos.
Agora
resolva este:
Um gato persegue um rato; enquanto o rato dá
5 pulos, o gato dá 3, porém 1 pulo do gato equivale a 2
pulos do rato. O rato leva uma dianteira equivalente a 50 pulos do
gato. Quantos pulos o gato deverá dar para alcançar o
rato?
Resposta: o gato deverá
dar 300 pulos.
3
Se 0 < k < 1, então o valor da
expressão
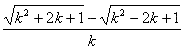
é igual a:
a) 0
b) 1
c) 2
d) 2/k
e) k
Solução:
Observe que pela condição
dada para k, ele é um número real entre 0 e 1, e por
conseqüência k + 1 > 0 e k – 1 <
0.
Observe também que k2 + 2k + 1 = (k + 1)2
e k2 – 2k + 1 = (k –
1)2
Substituindo na expressão dada fica:
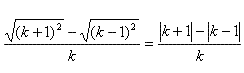
Se necessário, verifique a
definição de módulo
de um número real.
Ora, da definição de
módulo infere-se que, como k + 1 é positivo |k +
1| = k + 1 e como k – 1 é negativo, |k – 1| =
– (k – 1) = – k + 1.
Substituindo novamente, fica: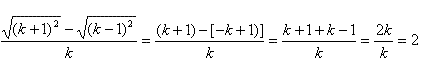
Notas:
1
– observe que k está situado entre 0 e 1 e portanto, é
diferente de zero, o que torna possível dizer que 2k / k = 2.
Portanto, a alternativa correta é a de letra C.
2 – se
k fosse igual a zero, teríamos 2k / k = 0 / 0 e não
poderíamos neste caso afirmar que o resultado seria 2, pois
0/0 poderia assumir qualquer valor. O símbolo 0/0 é
conhecido como uma indeterminação matemática.
3
– esta questão simples foi enviada por um estudante que
achou a solução 2/k por não ter observado corretamente as
propriedades da função módulo.
Agora
resolva este:
Se k < –1, então o valor da expressão
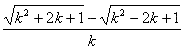 é igual a:
é igual a:
a) 0 b)
1 *c) -2/k d) 2/k e) k
4
UESB 2007.1 – Um cliente pagou 40 %
de uma dívida de x reais. Sabendo-se que R$300,00
correspondem a 20 % do restante a ser pago, é correto afirmar
que o valor de x é igual a
(01) 3750
(02) 3000
(03)
2750
(04) 2500
(05) 2050
Nota: UESB –
Universidade Estadual do Sudoeste Baiano
Solução:
Sendo
x o valor total da dívida, como foi pago 40% de x, restou
(100% - 40%) de x ou seja: 60% de x = 60% . x = 0,60x.
Pelo
enunciado, 20% do restante é igual a 300, ou seja: 20 % de 60%
de x = 0,20 . 0,60 . x = 0,12x = 300. Logo,
x = 300 / 0,12 = 30000
/ 12 = 15000 / 6 = 5000 / 2 = 2500.
5 UESB 2007.1 –Em uma campanha de Natal foram distribuidos entre algumas fam�lias de uma comunidade, 144 brinquedos, 192 pares de sapatos e 216 camisas. A distribui��o foi feita de modo que o maior n�mero poss�vel de fam�lias fossem contempladas e todas recebessem o mesmo n�mero de brinquedos, o mesmo n�mero de pares de sapatos e o mesmo n�mero de camisas. Considerando-se que cada fam�lia recebeu x brinquedos e y pares de sapatos, pode-se afirmar que o valor de x + y � igual a:
01) 24
02) 14
03) 12
04) 8
05) 6
Solução:
Trata-se de um problema t�pico de aplica��o do MDC - M�ximo Divisor Comum. Ora, MDC(144, 192, 216) = 24. Ent�o, ser�o 144/24 = 6 brinquedos, 192/24 = 8 pares de sapatos e 216/24 = 9 camisas para cada fam�lia. Do enunciado da quest�o infere-se ent�o x = 6 e y = 8 e, portanto, x + y ser� igual a 14, o que nos leva � alternativa (02). Se voc� quiser revisar MDC, visite o arquivo M�ximo Divisor Comum. Para retornar a esta p�gina, clique em VOLTAR no seu navegador.
6 – Um rato est� 30 metros � frente de um gato que o persegue. Enquanto o rato corre 8 metros, o gato corre 11 metros. Qual a dist�ncia que o gato ter� de percorrer para alcan��-lo?
Solução:
Seja g a dist�ncia percorrida pelo gato num tempo t e seja r a dist�ncia percorrida pelo rato no mesmo intervalo de tempo.
Poderemos escrever: g = 11t e r = 30 + 8t. O gato encontrar� o rato quando g = r, ou seja: 11t = 30 + 8t. Da� vem, 11t - 8t = 30 ou seja, 3t = 30, de onde tiramos t = 10. Substituindo em g = 11t vem, finalmente: g = 11.10 = 110 metros.
Resposta: o gato alcan�ar� o rato a 110 metros do ponto de partida.
7 – Um gato est� 72 metros � frente de um cachorro que o persegue. Enquanto o gato corre 7 metros, o cachorro corre 9 metros. Quantos metros o cachorro dever� percorrer at� ficar a 12 metros do gato?
Solução:
Sendo g a dist�ncia percorrida pelo gato num tempo t, poderemos escrever: g = 72 + 7t. Analogamente, sendo c a dist�ncia percorrida pelo cachorro no mesmo tempo t, vem: c = 9t. Ora, o cachorro estar� a 12 metros do gato quando g - c = 12 ou seja: (72 + 7t) - 9t = 12. Da� vem, 72 - 2t = 12 ou 2t = 60; portanto t = 60/2 = 30.
Substituindo este valor em c = 9t vem finalmente: c = 9.30 = 270.
Resposta: o cachorro estar� a 12 metros do gato ap�s ter percorrido 270 metros. Fa�a as contas para saber que o cachorro alcan�ar� o pobre gato ap�s ter percorrido 324 metros. A� ser� briga na certa!
Nota: aqui em casa - nestas f�rias de janeiro 2012, a cadela "dalila" (de Eduardo - meu filho, em f�rias) e o gato "pacheco" - residente aqui j� h� algum tempo, brigam de fazer d�! Por enquanto, o "pacheco" est� sofrendo fragorosa derrota! rarar�...
Paulo Marques, 16
de janeiro de 2007 - editado em 08 de janeiro de 2012.
VOLTAR