Resolver a seguinte inequação em R, conjunto dos números reais.
![]()
SOLUÇÃO:
Podemos escrever:
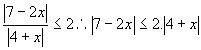
Observe que esta transformação algébrica
somente foi possível devido ao fato
do denominador ser um número positivo para x ¹
- 4. Lembre-se que o módulo é sempre
positivo ou nulo.
Nestas condições, poderemos quadrar - elevar ao quadrado - ambos os membros da desigualdade acima, obtendo:
49 - 28x + 4x2 £
4(16 + 8x + x2)
49 – 28x + 4x2 £
64 + 32x + 4x2
Cancelando os termos semelhantes 4x2
em ambos os membros, vem:
- 28x – 32x £
64 - 49
- 60x £
15
Multiplicando ambos os membros da desigualdade acima por –1, o sentido da desigualdade muda e teremos:
60x ³
- 15
x ³
-15/60
x ³
- ¼
Logo, o conjunto solução da inequação
dada no Universo dos Números Reais será:
S = {xÎ
R; x³ ¼}
= [1/4, ¥ ) (intervalo
real dos números maiores ou iguais a ¼).
Agora, coloco a seguinte questão: Se fosse dito no enunciado que o conjunto universo fosse o conjunto dos naturais, qual seria o conjunto solução da inequação dada?
Ora, já sabemos que x ³
¼. Logo, em N = {0, 1, 2, 3, 4, 5, ...} = conjunto dos números
naturais, teríamos que selecionar apenas as
soluções que pertencem ao conjunto N.
Teríamos, então:
S = {1,2,3,4,5,6,7, ...} = N* = N – {0}.
Lembrete: O conjunto
solução (ou conjunto verdade) de uma equação
ou inequação, depende do conjunto universo adotado. Assim
é que, por exemplo, a equação 3x – 2 = 0, tem conjunto
solução
S = {2/3} no universo R dos números reais,
porém em N conjunto dos naturais ou Z conjunto dos inteiros (positivo,
negativo ou nulo) o conjunto solução da mesma equação
seria vazio ou seja
S = f (conjunto vazio, ou seja um conjunto sem elementos), pois 2/3=0,6666... não é natural, nem inteiro.
Perceberam?
É muito importante perceber isto!
Paulo Marques - Feira de Santana
- BA - 02 de novembro de 1998