UEFS – Universidade Estadual de Feira de Santana

NOTA:
Prova com 25 questões objetivas de Matemática, 25 de História e 25 de Geografia, para ser resolvida em 4h.

CONTINUAÇÃO: Questões de 11 a 15

Questão 11 – Sabendo-se que, entre os números 13 e 694, existem x múltiplos de 11, x é igual a:

(01) 64
(02) 63
(03) 62
(04) 61
(05) 60

SOLUÇÃO:
Ora, os múltiplos de 11, formam uma PA de razão 11. O primeiro múltiplo de 11 maior do que 13 é 22; Precisamos saber qual o maior múltiplo de 11, menor do que 694. Dividindo 694 por 11 obtemos quociente 63 e resto 1. Logo, o múltiplo procurado será igual a 63x11 = 693.
Logo, temos a PA:
(22, 33, 44, ... , 693)
Usando a fórmula do termo geral da PA, ou seja: a_n = a₁ + (n – 1) r e substituindo os valores conhecidos, vem:
693 = 22 + (n – 1).11, onde n é o número de termos procurado e, portanto igual ao x do problema. Efetuando os cálculos, vem: n = 62, o que nos leva à alternativa (03).

Questão 12 – As medidas, em metros, dos lados de um triângulo são expressas por x + 1, 2x e x² e estão em progressão geométrica, nessa ordem. O perímetro do triângulo, em metros, mede:

(01) 9
(02) 9,5
(03) 19
(04) 28
(05) 30

SOLUÇÃO:
Temos a seguinte PG: (x + 1, 2x, x²). Usando o conceito de PG, podemos escrever:
2x/(x+1) = x²/(2x) [reveja PG nesta página, se necessário].
Daí, vem, usando as propriedades de proporção: (produto dos meios = produto dos extremos). Lembram-se?
4x² = (x+1).(x²) ; para x ¹ 0, podemos simplificar a expressão anterior, dividindo ambos os membros por x² , resultando: 4 = x + 1 \ x = 3.
Sendo x = 3, os lados do triângulo serão:
4, 6, 9 (uma PG de razão 3/2)
Sendo o perímetro de um triângulo, igual à soma das medidas dos seus lados, vem:
Perímetro = 4 + 6 + 9 = 19, o que nos leva à alternativa (03).

Questão 13 – Se f é uma função tal que f(x + 2) = x³ – 8, para todo x Î R, então f(x) é igual a

(01) x³ + 2x² + 2x
(02) x³ – 6x² + 12x – 16
(03) x³ + 6x² + 12x
(04) x³ – 3x² + 3x – 9
(05) x³ + 3x² + 3x – 7

SOLUÇÃO:
Façamos x + 2 = t. Daí, vem: x = t – 2
Substituindo, fica:
f(t) = (t – 2)³ – 8
f(t) = t³ – 3.t².2 + 3.t.2² – 2³ – 8 = t³ – 6t² + 12t – 8 – 8 = t³ – 6t² + 12t – 16
Portanto, f(x) = x³ – 6x² + 12x – 16, o que nos leva à alternativa (02).

Questão 14 – O domínio da função é o conjunto

(01) (-¥ , -1) È [3, ¥ )
(02) (-1, 3) È [4, ¥ )
(03) (-1, 3] È (4, ¥ )
(04) (-¥ , -1) È (4, ¥ )
(05) (4, ¥ )

SOLUÇÃO:
Como só existe raiz quadrada real de número positivo ou nulo, deveremos ter:
(2^x – 8)/(x² – 3x – 4) ³ 0
Esta é uma inequação quociente. Vamos resolve-la:
Inicialmente, vamos determinar os zeros (ou raízes) do numerador e denominador.
2^x – 8 ® raiz = 3, pois 2³ – 8 = 0
x² – 3x – 4 ® raízes: 4 e – 1
Vamos então construir a seguinte tabela, observando os sinais do numerador e denominador da desigualdade acima:

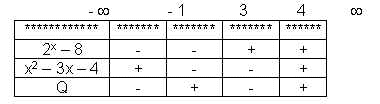
O sinal do quociente Q é positivo conforme tabela acima.
Observe que os números –1 e 4 anulam o denominador x² – 3x – 4, portanto não podem pertencer ao domínio da função.
Portanto, o domínio da função dada será:
D = (-1, 3] È (4, ¥ ), o que nos leva a alternativa (03).

Questão 15 – Se então f(-3) é igual a:

(01) –11
(02) –7
(03) 7
(04) 11
(05) 12

SOLUÇÃO:
Observe que a expressão que define a função, pode ser escrita como:
f(x) = x^6/3 – 6/x = x² – 6/x (Lembram-se de potências de expoentes fracionários?)
Portanto, f(-3) = (-3)² – 6/(-3) = 9 + 2 = 11, o que nos leva à alternativa (04).

Paulo Marques

VOLTAR