ITA – 1965) Dentro de um quadrado de lado a existem cinco círculos não superpostos de mesmo raio r. O centro de um dos círculos coincide com o centro do quadrado e ele tangencia os outros quatro círculos cada um dos quais tangencia dois lados do quadrado (cada um está num canto do quadrado). Exprimir r em termos de a.
Solução:
A figura a seguir, reflete o enunciado da questão.
Nota: a figura está parecendo um retângulo mas,
acreditem, eu quis desenhar um quadrado! eh eh eh
... .
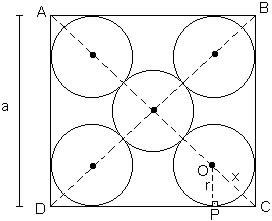
No triângulo retângulo
PCO, temos: PC2 + PO2 = OC2 , pelo teorema de
Pitágoras.
Vê-se
que o triângulo PCO é isósceles, pois os lados PO e PC possuem a mesma
medida, uma vez que o ângulo de vértice C mede 45º. Isto é verdadeiro,
porque AC é uma diagonal do quadrado. Temos então: OP = r
e PC = r.
r2 + r2 = x2
2.r2 = x2 \
x = r.Ö2
Novamente pelo teorema de Pitágoras, poderemos escrever para o triângulo ADC:
AD2 + DC2
= AC2
Observe que:
AD = a
DC = a
AC = 2x + 4r = 2. r.Ö2
+ 4r = (2 Ö2
+ 4).r
Substituindo e desenvolvendo, vem:
a2 + a2
= [(2 Ö2
+ 4).r]2
2.a2 = [(2.Ö2 + 4).r]2
Extraindo a raiz quadrada de ambos os membros, fica:
Ö2.a = 2.Ö2 + 4).r
Daí, vem:
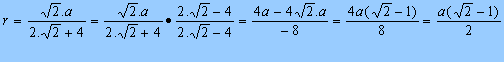
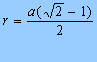
que é a resposta do problema proposto.
Observe que sendo Ö2
»
1,414, efetuando as contas chegaremos a:
r
»
0,21 a ou seja, o raio
r vale
aproximadamente 21% do comprimento do lado do quadrado.
Paulo Marques, Feira de Santana - BA, 03/11/2001 – editado em 09/10/2011.