Funções Exponenciais

1 – Sabemos de aulas anteriores  que, dado o número real a e sendo n um número natural maior ou igual a 2, poderemos definir: 
a ⁿ = a.a.a.a. ... . a , onde o termo a repete-se n vezes. O termo a é denominado, historicamente, como base  e n , expoente.
Assim, a² = a.a , a³ = a.a.a,  a⁴ = a.a.a.a , ... , e assim sucessivamente.
Exemplos:
2³ = 2.2.2 = 8
(-5)³ = (-5).(-5).(-5) = (+25).(-5) = -125
0¹⁰⁰ = 0.0.0. ... 0 = 0
(√2).(√2) = √4 = 2

Nota: para ampliar o conceito e sem nenhum prejuízo para a Matemática, definem-se adicionalmente que: a¹ = a  e que  a⁰ = 1, para qualquer número real a.
Exemplos:  7⁰ = 1, (-13)⁰ = 1, 10¹ = 10, 1¹ = 1, etc

2 – As seguintes propriedades são facilmente demonstráveis usando a definição do item (1) acima, para a, b, reais e m, n inteiros positivos. (Em a realidade, as propriedades seguintes são válidas para m ,  n quaisquer (reais ou complexos), o que adiantamos para vocês, aqui,  apenas por uma conveniência didática) :

P1) a^m . aⁿ = a^m+n
P2) a^m / aⁿ = a^m-n
P3) (a.b)ⁿ = aⁿ .bⁿ
P4) (a ^m)ⁿ = a^m.n
P5) (a/b)ⁿ = aⁿ /bⁿ , para b ≠ 0.

Exemplos:

a)2³.2⁵ = 2³⁺⁵ = 2⁸ = 2.2.2.2.2.2.2.2.2 = 64
b) 2⁷/2³ = (2^7-3) = 2⁴ = 2.2.2.2 = 16
c) (2.5)³ = 2³.5³ = 2.2.2.5.5.5 = 8.125 = 1000
d) (100/20)³ = 100³/20³ = 5³ = 5.5.5 = 125

Nota: Partindo-se da premissa (argumento) de que se A = B então B = A, é bastante conveniente “enxergar” as propriedades P1, P2, P3, P4 e P5 acima, também no sentido da direita para a esquerda, ou seja:

P’1) a^m+n = a^m . aⁿ
P’2) a^m-n = a^m / aⁿ
P’3) aⁿ .bⁿ = (a.b)ⁿ
P’4) a^m.n = (a ^m)ⁿ
P’5) aⁿ /bⁿ = (a/b)ⁿ , para b ≠ 0.

Por exemplo, às vezes é mais prático (para a resolução de problemas) concluir que (1000² /50²) = (1000/50)² =20² = 20.20 = 400, do que o contrário.

3 – Expoente negativo: ampliando o conceito

Todas as definições acima, consideraram os expoentes sendo números inteiros positivos ou nulo. E se o expoente for negativo? Bem, neste caso, partindo-se do princípio de que a⁰ = 1  poderemos imaginar a seguinte operação: a⁰ / aⁿ .

Ora, pela propriedade P5 acima, poderemos escrever:
(a⁰ / a ⁿ) = a^0-n = a^-n
E como a⁰ = 1, vem finalmente: 1/aⁿ = a^-n

Assim, lembrando que se A=B então B=A, poderemos concluir:

a^-n = 1 / aⁿ

Nota: claro que o número a tem que ser diferente de zero. Lembre-se que não há divisão por zero na Matemática! Experimente dividir uma maçã para zero pessoas! Claro que não haverá nenhuma forma de fazê-lo!

4 –   Expoente fracionário: ampliando o conceito um pouco mais

Seja a potencia  a^x/y onde a é um número real  e  x e y números inteiros.
Fazendo a^x/y = F, teremos elevando ambos os membros ao expoente y fica:
(a^x/y) ^y = F ^y , de onde deduz-se imediatamente que a^x = F^y .
Ora, sabemos que se A ⁿ = B, então  A = ⁿ√B. Logo, poderemos escrever que F = ^y√a^x e, como a ^x/y = F, concluímos finalmente que:

a ^x/y = ^y√a^x

Exemplos:
16^1/2 = √16 = 4
8^2/3 = ³√8² = ³√64 = 4, etc

5 – A função exponencial
Seja  0 < a ≠ 1, ou seja: a  é um número positivo e diferente de 1.
Define-se a função exponencial simples em R (conjunto dos números reais) como sendo a função f: R ® R ; y = f(x) = a^x .
Exemplos: y = 2^x , y = (1/3)^x , y = (√2)^x , etc

Nota: a exigência de que 0 < a ≠ 1 , decorre do fato de que se a = 1, teríamos y = 1^x = 1 (trata-se neste caso da função constante 
y = 1, que obviamente não é uma função exponencial); se a = 0, teríamos y = 0^x = 0, para x>0 ; se a < 0, por exemplo a = -2, teríamos y = (-2)^x , que não seria definida para todo x Î R (conjunto dos números reais) pois por exemplo, para x = ½ ficaria 
y = √(-2) que não é um número real. Então, para que y = a^x seja uma função exponencial é obrigatório que a base a seja positiva e diferente de 1.

5.1 – Propriedades da função y = a^x , 0 < a ≠ 1

P1) a inversa da função exponencial y = a^x é a função logarítmica y = log_ax

P2) se  a > 1, a função y = a^x é crescente. Isto pode ser facilmente visualizado no gráfico da função exibido abaixo onde estão representadas a função exponencial e a sua inversa (a função logarítmica).
 

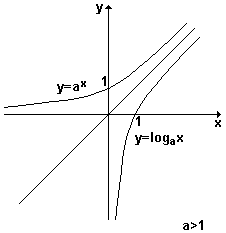
P3) se 0 < a < 1, a função exponencial y = a^x é decrescente. Isto pode ser facilmente visualizado no gráfico da função exibido abaixo onde estão representadas a função exponencial e a sua inversa (a função logarítmica).

 

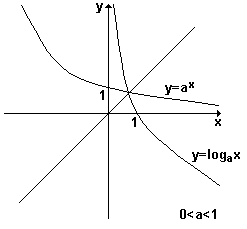
P4) O gráfico da função y = a^x passa sempre no ponto (0,1), pois para x = 0, vem y = a⁰ = 1. Portanto, o gráfico de qualquer função exponencial do tipo y = a^x  intercepta (corta) o eixo das ordenadas (eixo dos y) no ponto de ordenada 1.

As funções exponenciais possuem muitas aplicações no mundo físico, já que muitas grandezas apresentam variação exponencial a exemplo do crescimento de uma população, do crescimento do número de bactérias numa cultura, do crescimento do dinheiro por juros compostos, etc. Veremos na seqüência, exemplos que ilustram estes fatos.

Exercícios resolvidos

E1 – Qual o domínio da função exponencial  y = 2^x ?

Solução: sabemos que o domínio de uma função y = f(x) é o conjunto de valores que podem ser atribuídos a x. Observe que x sendo um expoente, ele poderá assumir qualquer valor e, portanto, o domínio da função dada é o conjunto dos números reais, ou seja: 
D = R.

E2) Qual o conjunto imagem da função y = 2^x ?

Solução: sabemos que o conjunto imagem de uma função y = f(x) é o conjunto de todos os valores que podem ser assumidos por y. Ora, como y = 2^x e x Î R, vemos facilmente que 2^x será sempre um número positivo e, portanto, como y = 2^x , concluímos que y será sempre positivo. Logo, o conjunto imagem da função dada será igual a Im = {x ÎR | x > 0}. Este conjunto pode também ser representado na forma Im = R₊^* , onde o sinal de asterisco, por convenção matemática, exclui o zero.

E3) Chama-se equação exponencial toda equação cuja incógnita figura num expoente. Nestas condições, pede-se resolver as seguintes equações:

a)  4^x – 20.2^x + 64 = 0

Solução: Sabemos que 4^x = (2²)^x = (2^x)² . Utilizando o artifício de fazer 2^x = y (isto chama-se mudança de variável) vem, substituindo:  y² – 20y + 64 = 0. Ora, esta é uma equação do segundo grau  cujas raízes são y = 16 ou y = 4. Substituindo na mudança de variável feita acima, teremos: 2^x = 16 ou 2^x = 4, de onde tiramos imediatamente que x = 4 ou x = 2. Portanto, o conjunto solução da equação proposta é S = {2; 4}.

b) 2^x - 3 = (2^x - 3)²

Solução: Fazendo 2^x - 3 = y, vem substituindo: y = y² . Daí vem que y² – y = 0 , o que é equivalente a y(y – 1) = 0 . Ora, para que o produto seja nulo deveremos ter y = 0 ou y = 1. Voltando à mudança de variável teremos: 2^x – 3 = 0  ou 2^x – 3 = 1. Vamos resolver cada uma separadamente.
2^x – 3 = 0 Þ 2^x = 3 ; da teoria dos logaritmos tiramos imediatamente que  x = log₂3
2^x – 3 = 1 Þ 2^x = 4, de onde tiramos imediatamente que x = 2. Portanto, o conjunto solução da equação proposta é S = {2; log₂3}.

c) 3^x+1 + 81/3^x = 36

Solução: A equação dada pode ser reescrita como: 3^x . 3¹ + 81/3^x – 36 = 0
Fazendo a mudança de variável 3^x = y vem: 3y + 81/y – 36 = 0
Multiplicando ambos os membros por y ≠ 0 (observe que y está no denominador e portanto, não pode ser igual a zero), obteremos: 3y² + 81 – 36y = 0
Arrumando a igualdade anterior fica: 3y² – 36y + 81 = 0. Vejam que podemos simplificar a equação, dividindo ambos os membros por 3, resultando:
y² – 12y + 27 = 0 ; ora, esta é uma equação do segundo grau cujas raízes são y = 9 ou y = 3. Voltando à mudança de variável teremos: 3^x = 9  ou 3^x = 3. Da primeira vem que x = 2 e da segunda vem que x = 1. Portanto, o conjunto solução da equação proposta é S = {2; 1} ou de uma forma equivalente: S = {1; 2}.

E4) O crescimento de certa cultura de bactérias obedece à função f(t) = C.e^kt , onde f(t) é o número de bactérias no tempo t ≥ 0, C e k são constantes positivas e e é a base do sistema de logaritmos neperianos. Se o número inicial de bactérias for igual a N  e duplica-se depois de 4 horas, determine em função de N, o número de bactérias ao fim de 8 horas.

Solução:  Temos pelo enunciado: f(0) = N (número de bactérias no instante inicial t = 0). Substituindo na expressão dada fica: N = C.e^k.0  , de onde tiramos N = C.1 = C .
Logo, o número de bactérias no instante t = 0 é igual a N = C ou também C = N.

Ainda pelo enunciado, temos f(4) = 2N, onde t = 4. Poderemos escrever:
2N = C.e^k.4 ;  substituindo C por N (do resultado anterior), fica:
2N = N . e^4k  ; daí vem simplificando: 2 = e^4k . Daí tiramos: 4k = log_e2 =ln2 , de onde vem: k = (log_e2) / 4 = (ln2) /4. Substituindo os valores encontrados para C e k na expressão dada, vem: f(t) = N.e^{[(ln2)/ 4]t}
Ora, o problema pede para calcular o valor de f(8) ou seja:
f(8) = N.e^{[(ln2) / 4]8} = N.e^2ln2 = N.e^ln4 = N.4 = 4N.

Portanto, ao final das 8 horas, o número de bactérias será igual a 4 vezes o número inicial.
Comentários: lembre-se de logaritmos que a^loga^N = N e, portanto, e^ln4 = 4, onde ln4 = log_e4.

Agora resolva estes:

Repitam as  soluções dos problemas resolvidos acima. Somente pegando no lápis ou na caneta, é que vocês conseguirão fixar os conceitos. A leitura somente, dará apenas uma tênue e irreal idéia do entendimento.

Paulo Marques, Feira de Santana - BA - 09 de Junho de 2007. Editado em 13/11/10.

VOLTAR