| Teorema dos Senos - TS |
Considere a figura abaixo, onde vemos um triângulo ABC inscrito numa circunferência de raio R. Observe que também podemos dizer que a circunferência está circunscrita ao triângulo ABC.
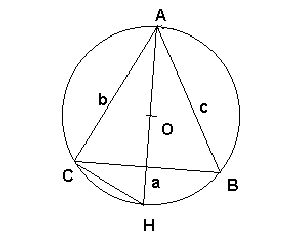 Na figura acima, temos:
Na figura acima, temos:
AH = diâmetro da circunferência = 2R
(R = raio)
AO = OH = raio da circunferência = R
Medidas dos lados do triângulo ABC:
AB = c, BC = a e AC = b.
Para deduzir o teorema
dos senos, vamos iniciar observando que
os ângulos H e B são congruentes ou seja possuem a mesma medida,
pois ambos estão inscritos no mesmo arco CA. Além disso,
podemos afirmar que o ângulo ACH é reto (90º), pois AH é um
diâmetro. Portanto o triângulo ACH é um triângulo retângulo.
Podemos então escrever:
sen H = sen B = cateto oposto / hipotenusa = AC / AH = b/2R
Logo, fica: sen B = b / 2R e, portanto, b/senB = 2R.
Analogamente chegaríamos às igualdades
c/senC = 2R
a/senA = 2R
Como estas três expressões são todas iguais a 2R,
poderemos escrever finalmente:
![]()
Esta expressão mostra que as medidas dos
lados de um triângulo qualquer são proporcionais aos senos dos
ângulos opostos a estes lados, sendo a constante de
proporcionalidade igual a 2R, onde R é o raio da circunferência
circunscrita ao triângulo ABC.
Este é o teorema dos senos – TS.
O teorema dos senos visto acima, permite a dedução de uma importante fórmula para o cálculo da área de um triângulo qualquer. Seja o triângulo ABC da figura abaixo, de altura h.
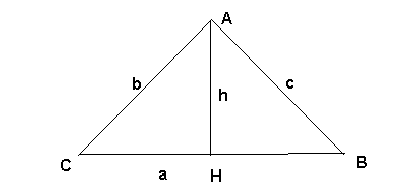
Sabemos que a área de um triângulo é
igual ao semiproduto da base pela altura:
S = 1/2 . base . altura . Logo,
S = 1/2 . a . h
Mas, no triângulo retângulo CAH, podemos escrever:
sen C = cateto oposto/hipotenusa = h/b
Þ h = b.senC
Substituindo na fórmula da área acima,
vem:
S = 1/2.a.b.senC
Mas, sabemos do teorema
dos senos que
c/senC = 2R, onde R é o raio da circunferência circunscrita ao
triângulo ABC. Logo: senC = c / 2R
Portanto, S = 1/2.a.b.c/2R = abc/4R.
Temos então a seguinte fórmula para o cálculo da área de um
triângulo qualquer:
![]()
onde a, b e c são as medidas dos lados do
triângulo e R é o raio da circunferência circunscrita
ao triângulo e S a área do triângulo.
Já sabemos da Geometria Plana, que a área de um triângulo ABC,
cujos lados medem respectivamente a, b e c, é dada pela fórmula:
![]()
onde p é o semiperímetro do triângulo ou seja: p = (a+b+c) / 2
Esta fórmula é conhecida comumente como Fórmula de Heron.
Heron de Alexandria – célebre geômetra grego. Viveu no século 1º
da era cristã.
Assim, substituindo o valor de S da fórmula anterior, na fórmula
S=abc/4R, encontraremos uma fórmula útil para o cálculo do
raio da circunferência circunscrita a um triângulo qualquer de
lados a, b e c:
Temos: S = abc / 4R Þ R = abc / 4S
Portanto,
![]()
Onde p, conforme vimos acima é o semiperímetro
dado por p = (a+b+c)/2.
Exemplo de aplicação: Vestibular da Univ.
Federal do Ceará/1990
Seja R o raio do círculo circunscrito ao triângulo cujos lados
medem 10m, 17m e 21m. Determine em metros, o valor de 8R.
Solução:
Temos: a = 10, b = 17 e c = 21 Þ p = (10+17+21) / 2 = 24
Portanto, substituindo diretamente na fórmula acima, fica:
![]()
Como o problema solicita o valor de 8R, vem:
8R = 8.170/16 = 170/2 = 85.
Portanto, 8R = 85, que é a resposta do problema.
Resposta: 85m
Paulo Marques -
Feira de Santana - BA, nos idos de outubro 1997, com revisão em 30/09/06.
CONTINUAR
VOLTAR