Três círculos tangentes entre si

Determine o diâmetro X na figura abaixo, sabendo-se que os tres círculos são tangentes entre si.

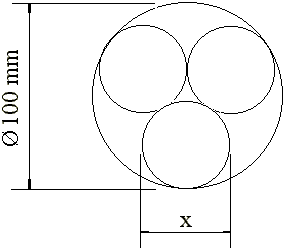
Solução:

Observando atentamente a figura abaixo, podemos escrever:

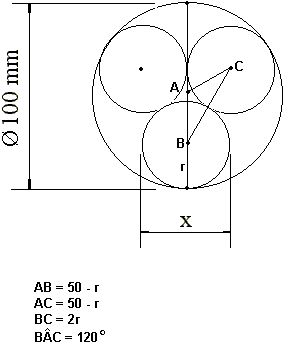
No triângulo isósceles ABC, teremos aplicando a lei dos cosenos:
BC² = AB² + AC² - 2.AB.AC. cos(BÂC)
(2r)² = (50 - r)² + (50 - r)² - 2.(50 - r).(50 - r) . cos 120º

Nota: cos 120º = - 1 / 2.
4r² = (50 - r)² + (50 - r)² + (50 - r)²
4r² = 3(50 - r)²
4r² / 3 = (50 - r)²
(2r / Ö 3)² = (50 - r)²
2r / Ö 3 = 50 - r
2r = 50Ö 3 - Ö 3.r
2r + Ö 3.r = 50.Ö 3
r(2 + Ö 3) = 50. Ö 3
Daí, vem:
r = 50. Ö 3 /(2 + Ö 3)
Racionalizando o denominador, vem:
r = 50(2Ö 3 - 3)
O diâmetro, sendo o dobro do raio, vem, finalmente:
X = 100(2Ö 3 - 3)

Portanto, o diâmetro procurado é igual a X = 100(2Ö 3 - 3) mm , que corresponde a aproximadamente
46,41 mm.

PAULO MARQUES - Feira de Santana - BA - nos idos de novembro de 1997, com revisão em 30/09/06.

CONTINUAR                VOLTAR