Transformações Geométricas - Questões Resolvidas

1. UFBA.76 - Sejam A = {-5/2, -5, 1/3, 17/6} e B o conjunto das imagens dos elementos de A pela composição das translações de vetores -3 e 1/2; então AÇ B é:
A) {1/3, -5}
B) {1/3, 17/6}
C) {5/2, -1/3, 17/6}
D) {-5/2, 1/3, -5}
E) {-5, 17/6, 1/3}

SOLUÇÃO:

Sabemos das aulas anteriores, que a composição de duas translações de vetores u e v, é uma nova translação de vetor u+v. Logo, a translação composta será de vetor igual a -3+1/2 = -6/2 + 1/2 = -5/2. Portanto, a translação composta será: T(x) = x - 5/2. Teremos então, para os elementos xÎ A:
Para x = -5/2 : T(-5/2) = -5/2 -5/2 = -10/2 = -5
Para x = -5 : T(-5) = -5 - 5/2 = -10/2 - 5/2 = -15/2
Para x = 1/3: T(1/3) = 1/3 - 5/2 = 2/6 - 15/6 = -13/6
Para x = 17/6 : T(17/6) = 17/6 - 5/2 = 17/6 - 15/6 = 2/6 = 1/3
Logo, o conjunto imagem B é igual a : B = {-5, -15/2, -13/6, 1/3}
Mas o problema pede AÇ B. Logo,
AÇ B = {-5/2, -5, 1/3, 17/6} Ç { -5, -15/2, -13/6, 1/3} = { -5, 1/3 } = { 1/3, -5} e portanto a alternativa correta é a letra A.

2 UFBA.76 - Dois vértices não consecutivos de um quadrado são (3,5) e (2, -1/2); as coordenadas do centro de simetria desse quadrado são:
A) (5, 9/2)
B) (5, 9/4)
C) (5, 11/4)
D) (5/2, 9/2)
E) (5/2, 9/4)

SOLUÇÃO:

Seja o quadrado da figura abaixo:

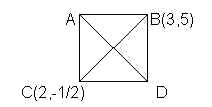
É óbvio que o centro de simetria do quadrado é o ponto de interseção das diagonais AD e CB. Logo, o centro de simetria é o ponto médio do segmento CB que é uma das diagonais do quadrado ABDC. Já sabemos da Geometria Analítica (veja nesta página), que o ponto médio de um segmento é um ponto cujas coordenadas são as médias aritméticas das abcissas e das ordenadas. Logo, o ponto médio, que neste caso é o centro de simetria do quadrado, será dado por:
ABCISSA = (2+3)/2 = 5/2
ORDENADA = (-1/2 + 5) / 2 = (9/2)/2 = 9/4.
Logo, o centro de simetria do quadrado é o ponto S(5/2, 9/4) e portanto, a alternativa correta é a letra E.

3 A translação T no plano, leva o ponto A(-2,3) no ponto B(4,6). Qual o transformado de P(2, -3) pela translação T?

SOLUÇÃO:

Teremos: T(x,y) = (x,y) + (a,b) onde (a,b) é o vetor translação no plano. Logo,
como T(-2,3) = (4,6) [dado do problema], vem:
(4,6) = (-2,3) + (a,b) Þ (a,b) = (4,6) - (-2,3) = (4+2, 6-3) = (6,3)
Portanto, sendo (6,3) o vetor translação, o transformado do ponto (2,-3) será:
T(2,-3) = (2,-3) + (6,3) = (2+6, -3+3) = (8, 0).
Resposta: o transformado do ponto (2, -3) pela translação T é o ponto (8, 0).

Nota: Para resolver problemas de transformações geométricas no plano (simetrias, translações ou homotetias), basta usar as mesmas fórmulas da transformação na reta, efetuando as mesmas operações, com os pares ordenados. Para isto, basta considerar que, dados dois pares ordenados (x,y) e (w,z), são válidas as três seguintes propriedades:
P1) (x,y) + (w,z) = (x+y, w+z)
P2) (x,y) - (w,z) = (x-y, w-z)
P3) Sendo kÎ R , é válido que k.(x,y) = (kx, ky)

4 Qual o transformado do ponto P(2,3) pela homotetia no plano de centro C(1,5) e de razão 4?

SOLUÇÃO:

Usando a fórmula da homotetia vista na aula anterior, adaptando-a para o caso de pares ordenados, vem:
(x', y') = [1- k].(c₁, c₂) + k.(x, y)
(x', y') = [1- 4].(1,5) + 4.(2,3) = -3.(1,5) + 4.(2,3) = (-3, -15) + (8, 12)
(x', y') = (-3+8, -15+12) = (5, -3)
Portanto, o homotético do ponto P(2,3) pela homotetia de centro (1,5) e razão 4 é o ponto (5, -3).

5 Qual o simétrico do ponto P(3, 5) pela simetria de centro C(1,4)?

SOLUÇÃO:

Usando a fórmula da simetria vista em uma aula anterior, adaptando-a para o caso de pares ordenados, vem:
(x', y') = 2(c₁,c₂) - (x,y)
(x', y') = 2(1,4) - (3,5) = (2,8) - (3,5) = (2-3, 8-5) = (-1, 3).
Resposta: (-1, 3)

6 Prove que o simétrico do ponto P(x,y) em relação à origem (0,0) do sistema de eixos coordenados é o ponto (-x, -y).

SOLUÇÃO:

Usando a fórmula de simetria vista acima, vem:
(x', y') = 2.(0, 0) - (x, y)
(x', y') = (0, 0) - (x, y)
(x', y') = (0-x, 0-y) = (-x, -y) , como queríamos demonstrar (c.q.d)
Ex: o simétrico do ponto P(-2,3) em relação à origem é o ponto (2, -3).

7 UFBA.72 - Seja (Oij) um sistema de referencia. Os pontos M' = O + 3i + 2j,
N' = O + i + j e P' = O + i são os transformados dos vértices M = O + 7i + 4j,
N = O + i + j e P = O + i - 2j de um triângulo por:

a) uma simetria de centro N
b) uma translação de vetor 4i+2j
c) uma homotetia de centro N e razão 1/3
d) uma homotetia de centro O e razão 1/3
e) nenhuma das respostas anteriores é válida

SOLUÇÃO:

Aqui neste problema aparece uma nova notação para pontos no plano, que entretanto é fácil de assimilar. Vamos explicar:
O = origem do sistema de coordenadas cartesianas = (0, 0)
i = vetor de módulo 1, no eixo dos x.
j = vetor de módulo 1, no eixo dos y
Assim, o ponto P = O + xi + yj é o mesmo que o ponto P(x, y). Simples, não é?

Exemplos:
P = O + 2i + 3j = (2,3)
Q = O + 2i - 3j = (2, -3)
R = O - 3j = (0, -3)
S = O + i = (1, 0), e assim sucessivamente.

Face ao exposto, podemos escrever os pontos dados no enunciado do problema, na forma usual de pares ordenados, conforme segue:
M'(3,2) N'(1,1) P'(1, 0) M(7, 4) N(1, 1) P(1, -2)

Este é o tipo de problema no qual temos de testar todas as alternativas.

Testei as alternativas e para economizar espaço, vou apenas demonstrar que a alternativa correta é a letra C. 

Vejamos:
A fórmula da homotetia no plano é, como já vimos:
(x', y') = [1 - k] . (c₁, c₂) + k. (x, y) onde k = razão da homotetia e (c₁, c₂) é o centro da homotetia.
A alternativa C fala numa homotetia de centro N(1,1) e razão k = 1/3.
Temos, então:
(x', y') = [1-1/3].(1,1) + 1/3(7,4) = 2/3(1,1) + 1/3(7,4) = (2/3, 2/3) + (7/3, 4/3)
(x', y') = (2/3+7/3, 2/3+4/3) = (3, 2) = M' (CONFORME ENUNCIADO DA ALTERNATIVA C).\
Analogamente, obteríamos os pontos N' e P', partindo dos pontos N e P pela homotetia de centro N(1, 1) e razão 1/3.

O entendimento deste problema requer bastante atenção. Faça os cálculos sugeridos acima, para que haja um perfeito entendimento.
Não desanime! MATEMÁTICA é inspiração mas, também, transpiração. Gaste um pouco de energia, QUE VALE A PENA!

Paulo Marques - Feira de Santana - BA, 02 de abril de 1995

VOLTAR