| Matemática não tem idade I (1969) - Uma moeda sobre a mesa, há quase 40 anos! |
Escola Preparatória de Cadetes do Exército - 1969
A questão que vou resolver a seguir, apareceu numa prova do Concurso de Admissão para a Escola Preparatória de Cadetes do Exército, no já quase remoto ano de 1969. Trata-se de uma questão de fácil interpretação, porém bastante interessante. Foi a questão 33 de um total de 50. Esta prova chegou em minhas mãos, em 1998, quase 30 anos após, através de um amigo que prestou tal concurso e perdeu!. Provando que o mundo dá voltas, apareceu uma questão similar no vestibular da UEFS- Universidade Estadual de Feira de Santana - primeiro semestre 2003. Veja no final do texto
Enunciado da questão:
Uma moeda de cinco centavos é colocada
sobre uma mesa.
O número de moedas de cinco centavos que se
podem colocar, tangentes ao redor dela é:
A) 6
B) 4
C) 5
D) 8
E) Nenhuma das respostas anteriores é verdadeira.
Solução:
O fato da moeda ser de cinco centavos, é
irrelevante.
O que importa na verdade, é o formato da moeda, que
é circular, ou seja a moeda é um círculo de raio r.
Para entender a resolução da questão, basta examinar a figura
abaixo:
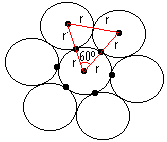
Nota: esta figura foi desenhada por um dos meus filhos, Rafael C. Marques, 12., hoje com 22!
Observe que, sendo os círculos
tangentes dois a dois,
o triângulo da figura é eqüilátero de lado 2r. Sabemos que os ângulos
internos de um triângulo eqüilátero são iguais a 60º.
Logo, caberão n moedas onde n = 360º/60º = 6.
Então, o número de moedas será igual a 6, o que nos leva à alternativa A.
Universidade Estadual de Feira de Santana - UEFS 2003 - 1º semestre
Um artesão usa peças circulares de mesmo diâmetro, para confeccionar tapetes circulares. Sabe-se que todas as peças são agregadas ao redor da peça central, tangenciando-a. Assim sendo, o número de peças necessárias para confeccionar cada tapete é igual a:
a) 9
b) 8
c) 7
d) 6
e) 5
Resposta: Alternativa C: 7 (observe que são 6 tangenciando + 1 tapete central = 7).
Veja a solução de outro problema de círculos tangentes no arquivo Cinco
círculos e um quadrado .
Paulo Marques - Feira de Santana - BA - 1998. Arquivo editado em 22/12/2008.