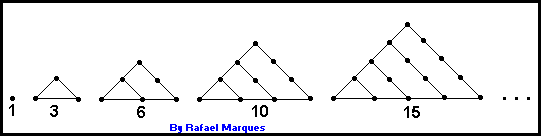
FGV – SP) Os números 1, 3, 6, 10, 15, ... são chamados de números triangulares,
nomenclatura esta justificada pela seqüência de triângulos:

a) determine uma expressão algébrica para o enésimo número triangular.
b) prove que o quadrado de todo número inteiro maior do que 1 é a soma de dois
números triangulares consecutivos.

Solução:

a) determine uma expressão algébrica para o enésimo número triangular.
Seja T_n o número triangular de ordem n ou seja, o n-ésimo ou enésimo número triangular.
Teremos, conforme enunciado da questão:
T₁ = 1
T₂ = 3
T₃ = 6
T₄ = 10 e assim sucessivamente. Desejamos achar T_n.

Observe que:
T₁ = 1
T₂ = 3 = 1 + 2 = T₁ + 2
T₃ = 6 = 3 + 3 = T₂ + 3
T₄ = 10 = 6 + 4 = T₃ + 4
T₅ = 15 = 10 + 5 = T₄ + 5
Observando atentamente as igualdades acima, podemos deduzir imediatamente que:
T_n = T_n-1 + n , ou seja, cada número triangular é a soma do anterior com o seu número
de ordem.

Somando membro a membro as igualdades acima, teremos:
T₁ + T₂ + T₃ + T₄ + T₅ + ... + T_n = 1 + T₁ + T₂ + T₃ + T₄ + ... + T_n-1 + 2 + 3 + 4 + 5 + ... + n
Cancelando os termos iguais nos dois membros, fica:
T_n = 1 + 2 + 3 + 4 + 5 + ... + n
Portanto, o enésimo número triangular é a soma de 1 a n.
Exemplo: T₇ = 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28

Ora, 1 + 2 + 3 + 4 + ... + n é a soma dos n primeiros termos de uma Progressão Aritmética de primeiro termo 1, razão 1 e último termo n. Pelo que já sabemos de P.A. poderemos escrever:

1 + 2 + 3 + 4 + 5 + ... + n = [n (n + 1)] / 2
Portanto,

T_n = [n (n + 1)] / 2

Está portanto respondido o item (a).

Exemplos de números triangulares:

Qual o centésimo número triangular?
T₁₀₀ = (100.101) / 2 = 5050

Qual o milésimo número triangular?
T₁₀₀₀ = 1000.1001 / 2 = 500500

Vamos agora responder o item (b):

b) Prove que o quadrado de todo número inteiro maior do que 1 é a soma de dois
números triangulares consecutivos.

Seja o número triangular T_n = [n (n + 1)] / 2 , expressão obtida no item anterior.
Os números triangulares são:
1, 3, 6, 10, 15, 21, 28, ... obtidos fazendo n = 1, 2, 3, 4, 5, 6, 7, ... na expressão acima.
Os quadrados dos números inteiros maiores do que 1 são:
4, 9, 16, 25, 36, 49, ...

Observe que realmente o quadrado de um número inteiro maior do que 1, é igual à soma
de dois números triangulares consecutivos, pois:
2² = 4 = 1 + 3 = T₁ + T₂
3² = 9 = 3 + 6 = T₂ + T₃
4² = 16 = 10 + 6 = T₄ + T₃
5² = 15 + 10 = T₅ + T₄ e assim sucessivamente.

Então, de uma forma genérica, n² = T_n + T_n-1 , para n > 1 e inteiro.
Vamos provar isto.

Ora, já sabemos que T_n = [n (n + 1)] / 2 .

Para T_n-1, teremos: T_n-1 = [(n-1)(n – 1 + 1)] / 2 = [(n – 1) . n] / 2

Então,

T_n + T_{n – 1} = [n (n + 1)] / 2 + [(n – 1) . n] / 2 = (n² + n) / 2 + (n² – n) / 2
Efetuando a soma indicada e simplificando obteremos finalmente:
T_n + T_{n – 1} = n² , o que comprova a afirmação do item (b).

Daí podemos inferir que a soma de dois números triangulares consecutivos é sempre
um quadrado perfeito.

Os números triangulares foram estudados por Pitágoras matemático e filósofo grego do século VI AC.

Poderemos também expressar um número triangular usando a Análise Combinatória.
Dos nossos conhecimentos de Análise Combinatória, poderemos escrever:

C_{n+1, 2} = (n + 1)! / (n + 1 – 2)!.2! = (n+1)! / (n – 1)!.2! = (n+1).n.(n-1)! / (n-1)!.2.1
Simplificando, obteremos:
C_{n+1, 2} = (n+1).n / 2 que é a mesma expressão para o enésimo número triangular, conforme vimos acima. Logo, poderemos concluir finalmente que:
T_n = C_{n+1, 2} para n = 1, 2, 3, 4, ...

Portanto, o número de combinações simples de (n + 1) elementos associados 2 a 2 resulta no número triangular T_n .

Se considerarmos uma reunião de n pessoas, na qual todos se cumprimentam entre si,
qual seria o total de cumprimentos?
Vamos achar a resposta em função dos números triangulares.
Ora, se A aperta a mão de B, isto é a mesma coisa de B apertar a mão de A . Portanto,
para saber o resultado, basta calcular o número de combinações simples de n elementos tomados dois a dois, ou seja:

C_{n, 2} = n! / (n – 2)!.2! = n (n – 1)(n – 2)! / (n – 2)!.2.1 = [n (n – 1)] / 2

Ora, n (n – 1) / 2 é exatamente o número triangular T_n-1 , pois:
Como T_n = n (n + 1) / 2, substituindo n por n – 1 vem exatamente:
T_{n – 1} = n (n – 1) / 2

Portanto, numa reunião de n pessoas na qual todos cumprimentam-se entre si, haverão
T_n-1 cumprimentos, onde T_{n -1} é um número triangular.

Por exemplo, numa reunião de 10 pessoas onde todos cumprimentam-se entre si,
teremos um total de T_{10 – 1} = T₉ = 9.10 / 2 = 45 cumprimentos, ou seja, o número triangular T₉.

Agora resolva este:
Prove que 3T_n + T_{n – 1} = T_{2 n} , onde T_n é um número triangular de ordem n.

Paulo Marques, 12 de abril de 2003 – Feira de Santana – Bahia - ampliado em 23/04/2005

VOLTAR
CONTINUAR