1 – Uma moeda é viciada, de forma que as caras são três vezes mais prováveis de aparecer do que as coroas. Determine a probabilidade de num lançamento sair coroa.
Solução:
Seja k a probabilidade de sair
coroa. Pelo enunciado, a probabilidade de sair cara é igual a
3k.
A soma destas probabilidades tem de ser igual a 1.
Logo, k
+ 3k = 1 \ k = 1/4.
Portanto, a
resposta é 1/4 = 0,25 = 25%.
2 – Uma moeda é viciada, de forma que as coroas são cinco vezes mais prováveis de aparecer do que as caras. Determine a probabilidade de num lançamento sair coroa.
Resposta: 5/6 = 83,33%
3 – Três estudantes A, B e C estão em uma competição de natação. A e B têm as mesmas chances de vencer e, cada um, tem duas vezes mais chances de vencer do que C. Pede-se calcular a probabilidades de A ou C vencer.
Solução:
Sejam p(A), p(B) e p(C), as
probabilidades individuais de A, B, C, vencerem. Pelos dados do
enunciado, temos:
p(A) = p(B) = 2.p(C).
Seja p(A) = k. Então,
p(B) = k e p(C) = k/2.
Temos: p(A) + p(B) + p(C) = 1.
Isto é explicado pelo fato de que a probabilidade de A vencer ou B vencer ou C vencer é igual a 1. (evento certo).
Assim, substituindo, vem:
k + k + k/2 = 1 \
k = 2/5.
Portanto, p(A) = k = 2/5, p(B) = 2/5 e p(C) = 2/10 = 1/5.
A probabilidade de A ou C
vencer será a soma dessas probabilidades, ou seja 2/5 + 1/5 =
3/5.
4 – Uma
moeda é viciada, de maneira que as CARAS são três
vezes mais prováveis de aparecer do que as COROAS. Calcule as
probabilidades de num lançamento sair COROA.
Resposta: 1/4.
5 – Um dado é viciado, de modo que cada número par tem duas vezes mais chances de aparecer num lançamento, que qualquer número ímpar. Determine a probabilidade de num lançamento aparecer um número primo.
Solução:
Pelo enunciado, podemos
escrever:
p(2) = p(4) = p(6) = 2.p(1) = 2.p(3) = 2.p(5).
Seja
p(2) = k. Poderemos escrever:
p(2) + p(4) + p(6) + p(1) + p(3) +
p(5) = 1, ou seja: a soma das probabilidades dos eventos elementares
é igual a 1.
Então, substituindo,
vem:
k + k + k + k/2 + k/2 + k/2 = 1 \
k = 2/9.
Assim, temos:
p(2) = p(4) = p(6) = 2/9
p(1)
= p(3) = p(5) = 2/18 = 1/9.
O evento sair número
primo corresponde a sair o 2, ou o 3 ou o 5. Logo,
p(2) + p(3) + p(5)
= 2/9 + 1/9 + 1/9 = 4/9.
6 – Use o mesmo enunciado anterior e determine a probabilidade de num único lançamento sair um número ímpar.
Resposta: 1/3
7 – Um cartão é retirado aleatoriamente de um conjunto de 50 cartões numerados de 1 a 50. Determine a probabilidade do cartão retirado ser de um número primo.
Solução:
Os números primos de 1
a 50 são: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 e
47, portanto, 15 números primos.
Temos, portanto, 15
chances de escolher um número primo num total de 50
possibilidades. Portanto, a probabilidade pedida será igual a p = 15/50 = 3/10.
8 - Use o mesmo enunciado anterior e determine a probabilidade de numa única retirada, sair um cartão com um número divisível por 5.
Resposta: 1/5.
9 – Das 10 alunas de uma classe, 3 tem olhos azuis. Se duas delas são escolhidas ao acaso, qual é a probabilidade de ambas terem os olhos azuis?
Solução:
Existem C10,2 possibilidades de se escolher duas pessoas entre 10 e, existem C3,2 possibilidades de escolher duas alunas de olhos azuis entre as três. Logo, a probabilidade procurada será igual a:
P = C3,2 / C10,2 = (3.2/2.1)/(10.9/2.1) = 6/90 = 3/45 = 1/15.
Comentários sobre o cálculo de Cn,p.
Como já sabemos da Análise Combinatória ,
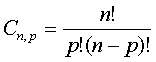
Esta é a forma tradicional de se calcular Cn,p.
Na prática, entretanto, podemos recorrer ao seguinte expediente: Cn,p possui sempre p fatores no numerador a partir de n, decrescendo uma unidade a cada fator e p fatores no denominador a partir de p, decrescendo uma unidade a cada fator.
Exemplos:
C10,4 = (10.9.8.7)/(4.3.2.1) = 210.
C8,3 = (8.7.6)/(3.2.1) = 56.
C16,3 = (16.15.14)/(3.2.1) = 560.
C12,4 = (12.11.10.9)/(4.3.2.1) = 495.
C10,5 = (10.9.8.7.6)/(5.4.3.2.1) = 252.
10 – Considere o mesmo enunciado da questão anterior e calcule a probabilidade de na escolha de duas alunas, nenhuma ter olhos azuis.
Resposta: 7/15.
Dica: como nenhuma das alunas deve ter olhos azuis, restam 10 – 3 = 7 alunas. Portanto, ...
Paulo Marques, 30 de dezembro de 2000.