Binômio de Newton Primeiro |
Considere o binômio

Sabendo-se que o termo independente de x é o quinto termo, pede-se determinar o valor de r e o termo independente de x.
Solução:
Podemos escrever:

Já sabemos que a fórmula do termo geral do desenvolvimento do binômio (w + b)n é dada por:

Onde temos o número binomial
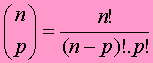
e o fatorial n! = 1.2.3.4.5. ... .n
Substituindo os valores de w = 1/x , b = ar.x2r e n = 36, fica:

Para que o termo seja independente de x, o expoente de x deve ser nulo. Logo, deveremos ter
8r – 32 = 0, de onde tiramos r
= 4.
O quinto termo T5 será então igual a:

Observe que x8.4-32 = x32-32
= x0 = 1.
Portanto, r = 4 e o termo independente
de x é igual a 58905 a16.