| Arrumando uma fila |
De quantos modos diferentes podem ser dispostas em fila (p+q) pessoas sendo p homens de alturas todas diferentes e q mulheres também de alturas diferentes, de modo que, tanto no grupo dos homens como no das mulheres, as pessoas se sucedam em alturas crescentes?
Solução:
Supondo os p homens e as q
mulheres ordenados segundo suas alturas crescentes, teremos ao
todo (p+q) pessoas. Ordenando-se os
p homens em p dos
(p+q)
lugares, as q mulheres ocuparão os q lugares restantes.
Ora, basta calcular então, o número de maneiras de preencher p
lugares entre os (p+q) lugares existentes, isto é, determinar
quantos subconjuntos de p elementos podem ser formados num
conjunto de (p+q)
elementos, com a condição de ordenamento crescente das alturas.
O número procurado será igual ao número de combinações possíveis de (p+q) elementos tomados p a p.
Logo:
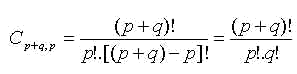
Portanto, p homens e q mulheres podem ser dispostos em fila em ordem crescente de altura, de (p+q)! / p!.q! maneiras distintas.
Exemplo de verificação:
Considere três homens e duas mulheres, com as seguintes alturas
em metros:
Pedro, com 1,76m = P
Rafael, com 1,77m = R
Eduardo, com 1,78m = E
Maria, com 1,75 m = M
Samantha, com 1,74m = S
Em termos de alturas temos:
E > R > P > M
> S
Pela fórmula acima, o número de
maneiras de dispor estas cinco pessoas em ordem crescente de
altura, será igual a:
n = (3+2)! / 3!.2! = 5! /3!.2! = 120/12 = 10.
São as seguintes, as 10 disposições possíveis,
considerando-se a ordem crescente de alturas:
01 – PREMS
02 – PRMES
03 – PRMSE
04 – MPRES
05 – MPRSE
06 – MPSRE
07 – PMRES
08 – PMRSE
09 – PMSRE
10 – MSPRE
Paulo Marques, Feira de Santana - BA - 29/06/2000.