Limites

A Teoria dos Limites, tópico introdutório e fundamental da Matemática Superior, será vista aqui, de uma forma simplificada, sem aprofundamentos, até porque, o nosso objetivo nesta página, é abordar os tópicos ao nível do segundo grau, voltado essencialmente para os exames vestibulares.
Portanto, o que veremos a seguir, será uma introdução à Teoria dos Limites, dando ênfase principalmente ao cálculo de limites de funções, com base nas propriedades pertinentes.
O estudo teórico e avançado, vocês verão na Universidade, no devido tempo.
Outro aspecto importante a ser comentado, é que este capítulo de LIMITES abordará o estritamente necessário para o estudo do próximo tópico: DERIVADAS.

O matemático francês - Augustin Louis CAUCHY - 1789/1857 , foi, entre outros, um grande estudioso da TEORIA DOS LIMITES. Antes dele, Isaac NEWTON - inglês - 1642 /1727 e Gottfried Wilhelm LEIBNIZ - alemão - 1646 /1716 , já haviam desenvolvido o Cálculo Infinitesimal.

DEFINIÇÃO

Dada a função y = f(x), definida no intervalo real (a, b), dizemos que esta função f possui um limite finito L quando x tende para um valor x₀, se para cada número positivo e , por menor que seja, existe em correspondência um número positivo d , tal que para
| x - x₀ | < d  , se tenha |f(x) - L | < e , para todo x ¹ x₀ .
Indicamos que L é o limite de uma função f( x ) quando x tende a x₀ , através da simbologia abaixo:
lim f(x) = L
x® x₀

Para revisar MÓDULO e FUNÇÕES, clique AQUI. Para retornar, clique em VOLTAR no seu BROWSER.

Exercício:
Prove, usando a definição de limite vista acima, que:
lim (x + 5) = 8
x® 3

Temos no caso:
f(x) = x + 5
x₀ = 3
L = 8.

Com efeito, deveremos provar que dado um e > 0 arbitrário, deveremos encontrar um d > 0, tal que, para  |x - 3| < d , se tenha |(x + 5) - 8| < e . Ora, |(x + 5) - 8| < e é equivalente a | x - 3 | < e .
Portanto, a desigualdade |x - 3| < d , é verificada, e neste caso d = e .
Concluímos então que 8 é o limite da função para x tendendo a 3 ( x ® 3) .

O cálculo de limites pela definição, para funções mais elaboradas, é extremamente laborioso e de relativa complexidade.
Assim é que, apresentaremos as propriedades básicas, sem demonstrá-las e, na sequência, as utilizaremos para o cálculo de limites de funções.

Antes, porém, valem as seguintes observações preliminares:

a) é conveniente observar que a existência do limite de uma função, quando x ® x₀ , não depende necessariamente que a função esteja definida no ponto x₀ , pois quando calculamos um limite, consideramos os valores da função tão próximos quanto queiramos do ponto x₀ , porém não coincidente com x₀, ou seja, consideramos os valores da função na vizinhança do ponto x₀ .
Para exemplificar, consideremos o cálculo do limite da função abaixo, para x ® 3.

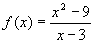
Observe que para x = 3, a função não é definida. Entretanto, lembrando que x² - 9 = (x + 3) (x - 3), substituindo e simplificando, a função fica igual a f(x) = x + 3, cujo limite para x ® 3 é igual a 6, obtido pela substituição direta de x por 3.

b) o limite de uma função y = f(x), quando x ® x₀, pode inclusive, não existir, mesmo a função estando definida neste ponto x₀ , ou seja , existindo f(x₀).

c) ocorrerão casos nos quais a função f(x) não está definida no ponto x₀, porém existirá o limite 
de f(x) quando x ® x₀ .

d) nos casos em que a função f(x) estiver definida no ponto x₀ , e existir o limite da 
função f(x) para x ® x₀ e este limite coincidir com o valor da função no ponto x₀, diremos que a 
função f(x) é CONTÍNUA no ponto x₀ .

e) já vimos a definição do limite de uma função f(x) quando x tende a x₀ , ou x ® x₀ . 
Se x tende para x₀ , para valores imediatamente inferiores a x₀ , dizemos que temos um limite à esquerda da função. Se x tende para x₀ , para valores imediatamente superiores a x₀ , dizemos que temos um limite à direita da função. Pode-se demonstrar que se esses limites à direita e à esquerda forem iguais, então este será o limite da função quando x ® x₀ .

Propriedades operatórias dos limites.

P1 - o limite de um soma de funções, é igual à soma dos limites de cada função.
lim ( u + v + w + ... ) = lim u + lim v + lim w + ...

P2 - o limite de um produto é igual ao produto dos limites.
lim (u . v) = lim u . lim v

P3 - o limite de um quociente de funções, é igual ao quociente dos limites.
lim (u / v) = lim u / lim v , se lim v ¹ 0.

P4 - sendo k uma constante e f uma função, lim k . f = k . lim f

Observações: No cálculo de limites, serão consideradas as igualdades simbólicas, a seguir, envolvendo os símbolos de mais infinito ( + ¥ ) e menos infinito ( - ¥ ), que representam quantidades de módulo infinitamente grande. É conveniente salientar que, o infinitamente grande, não é um número e, sim , uma tendência de uma variável, ou seja: a variável aumenta ou diminui, sem limite.

Na realidade, os símbolos + ¥ e - ¥ , não representam números reais, não podendo ser aplicadas a eles, portanto, as técnicas usuais de cálculo algébrico.

Dado b Î R - conjunto dos números reais, teremos as seguintes igualdades simbólicas:
b + (+ ¥ ) = + ¥
b + ( - ¥ ) = - ¥
(+ ¥ ) + (+ ¥ ) = + ¥
(- ¥ ) + (- ¥ ) = - ¥
(+ ¥ ) + (- ¥ ) = nada se pode afirmar inicialmente. O símbolo ¥ - ¥ , é dito um símbolo de indeterminação.
(+ ¥ ) . (+ ¥ ) = + ¥
(+ ¥ ) . 0 = nada se pode afirmar inicialmente. É uma indeterminação.
¥ / ¥ = nada se pode afirmar inicialmente. É uma indeterminação.

No cálculo de limites de funções, é muito comum chegarmos a expressões indeterminadas, o que significa que, para encontrarmos o valor do limite, teremos que levantar a indeterminação, usando as técnicas algébricas. Os principais símbolos de indeterminação, são:
¥ - ¥
¥ . 0
¥ / ¥
¥ ⁰
0 / 0
1¥
1^{- ¥}

Vamos agora calcular alguns limites imediatos, de forma a facilitar o entendimento dos exercícios mais complexos que virão em seguida:

a) lim (2x + 3) = 2.5 + 3 = 13
.....x® 5

b) lim (x² + x) = (+ ¥ )² + (+ ¥ ) = + ¥ + ¥ = + ¥
.....x® +¥

c) lim (4 + x³) = 4 + 2³ = 4 + 8 = 12
.....x® 2

d) lim [(3x + 3) / (2x - 5)] = [(3.4 + 3) / (2.4 - 5)] = 5
.....x® 4

e) lim [(x + 3) (x - 3)] = (4 + 3) (4 -3) = 7.1 = 7
.....x® 4

LIMITES FUNDAMENTAIS

A técnica de cálculo de limites, consiste na maioria das vezes, em conduzir a questão até que se possa aplicar os limites fundamentais, facilitando assim, as soluções procuradas. Apresentaremos a seguir - sem demonstrar - cinco limites fundamentais e estratégicos, para a solução de problemas.

Primeiro limite fundamental : O limite trigonométrico

Para revisar TRIGONOMETRIA, clique AQUI. Para retornar, clique em VOLTAR no seu BROWSER.

Intuitivamente isto pode ser percebido da seguinte forma: seja x um arco em radianos, cuja medida seja próxima de zero, digamos x = 0,0001 rad. Nestas condições, o valor de senx será igual a
sen 0,0001 = 0,00009999 (obtido numa calculadora científica).
Efetuando-se o quociente, vem: senx / x = 0,00009999 / 0,0001 = 0,99999 » 1.
Quanto mais próximo de zero for o arco x, mais o quociente (senx) / x se aproximará da unidade, caracterizando-se aí, a noção intuitiva de limite de uma função.

Exercício:

Observe o cálculo do limite abaixo:

Observe que fizemos acima, uma mudança de variável, colocando 5x = u, de modo a cairmos num limite fundamental. Verifique também que ao multiplicarmos numerador e denominador da função dada por 5, a expressão não se altera. Usamos também a propriedade P4 vista no início do texto.

Segundo limite fundamental : Limite exponencial

Onde e é a base do sistema de logaritmos neperianos, cujo valor aproximado é e » 2,7182818.
Para revisar LOGARITMOS, clique AQUI. Para retornar, clique em VOLTAR no seu BROWSER.

Exercício:

Observe o cálculo do limite abaixo:

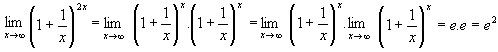
Terceiro limite fundamental : Conseqüência do anterior

Exercício:

Observe o cálculo do limite abaixo.
lim (1 + x)^5/x = lim [(1 + x)^1/x]⁵ = e⁵
x® 0 ................x® 0

Quarto limite fundamental : outro limite exponencial

Para a > 0.

Quinto limite fundamental

EXERCÍCIOS PROPOSTOS

Determine os seguintes limites:

a) lim (2 senx - cos2x + cotgx)
.....x® p /2
Resp: 3

b) lim (5 - 1/x + 3/x²)
.....x® ¥
Resp: 5

c) lim (4x³ - 2x² + 1) / (3x³ - 5)
.....x® ¥
Sugestão: divida numerador e denominador por x³.
Resp: 4/3

d) lim (senx / tgx)
.....x® 0
Resp: 1

e) lim (sen4x) / x
.....x® 0
Resp: 4

f) lim [(1 + 1/x)^{x + 3}
....x® ¥
Resp: e

g) lim [(1 + x)^m - 1] / mx
.....x® 0
Resp: 1

Paulo Marques - Feira de Santana - BA , 30/12/1999.

VOLTAR
CONTINUAR