| Derivadas I |
Derivada de uma função y = f(x) num ponto x = x0
Reveja o capítulo introdutório de
LIMITES, clicando AQUI.
Para retornar, clique em VOLTAR no seu BROWSER.
Considere a figura abaixo, que representa o gráfico de uma função y = f(x), definida num intervalo de números reais.
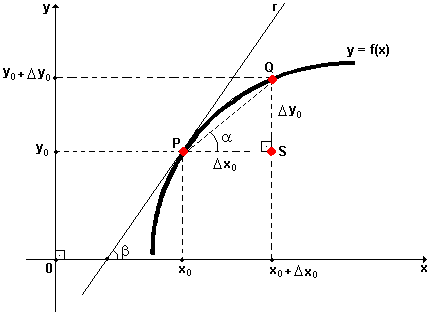
Observando a figura, podemos definir o seguinte quociente, denominado razão incremental da função y = f(x), quando x varia de x0 para x0 + D x0 :
![]()
Se você não entendeu porque o quociente
acima é igual à tg a , revise TRIGONOMETRIA, clicando AQUI.
Para RETORNAR, clique em VOLTAR no seu BROWSER.
Define-se a derivada da função y =
f(x) no ponto x = x0, como sendo o limite da razão
incremental acima, quando D x0 tende a zero, e é representada por f
' (x0) , ou seja:
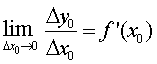
Notas:
a) a derivada de uma função y = f(x), pode ser
representada também pelos símbolos y ' ou dy/dx, notação introduzida por Wilhelm Gottfried Leibniz
- matemático alemão (1646 - 1716), contemporâneo do físico e matemático
inglês Isaac Newton ((1642-1727). As proezas dos dois gênios no Cálculo
Infinitesimal, você poderá ler no livro e: A HISTÓRIA DE UM NÚMERO, de autoria de Eli Maor - Editora
RECORD , traduzido para o português.
b) a derivada da derivada de uma função, é conhecida
com segunda derivada e é representada pelos símbolos y
'' ou d2y/dx2
.
Observe que quando D x0 ® 0 , o ponto Q no
gráfico acima, tende a coincidir com o ponto P da mesma figura.,
definindo a reta r , que forma um ângulo b com o eixo horizontal
(eixo das abscissa), e, neste caso, o ângulo SPQ = a .tende ao
valor do ângulo b .
Ora, quando D
x0 ® 0 , já vimos que o quociente D y0 / D x0
representa a derivada da função
y = f(x)
no ponto x0. Mas, o quociente D y0 / D x0
representa , como sabemos da Trigonometria, a tangente do ângulo
SPQ = a , onde P é o vértice do ângulo.
Quando D x0 ® 0 , o ângulo SPQ
= a , tende
ao ângulo b
.
Assim, não é difícil concluir que a derivada da função y = f(x) no ponto x = x0 , é igual numericamente à tangente do ângulo b . Esta conclusão será muito utilizada no futuro.
Podemos escrever então:
f '(x0)
= tgb
Guarde então a seguinte conclusão importante:
| A derivada de uma função y =
f(x) num ponto x = x0 , coincide numericamente
com o valor da tangente trigonométrica do ângulo
formado pela tangente geométrica à curva representativa
de y = f(x), no ponto x = x0. |
Estou falando há muito tempo em DERIVADAS, e ainda não calculei nenhuma!
Vamos lá!
Existem fórmulas para o cálculo das derivadas das funções - as quais serão mostradas no decorrer deste curso - mas, por enquanto, vamos calcular a derivada de uma função simples, usando a definição. Isto servirá como um ótimo exercício introdutório, que auxiliará no entendimento pleno da definição acima.
| Calcule a derivada da função y = x2 , no ponto x = 10. |
Temos neste caso:
y = f(x) = x2
f(x + D
x) = (x + D
x)2 = x2 + 2x.D x + (D x)2
f(x + D
x) - f(x) = x2 + 2x.D x + (D x)2 - x2 = 2x.D x + (D x)2
D y = f(x + D x) - f(x) = x2 + 2x.D x + (D x)2 - x2
= 2x.D x + (D x)2
Portanto,
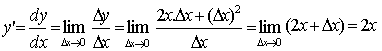
Observe que colocamos na expressão acima, D x em evidencia e,
simplificamos o resultado obtido.
Portanto a derivada da função y = x2 é igual a y '
= 2x .
Logo, a derivada da função y = x2, no ponto x = 10 ,
será igual a : y ' (10) = 2.10 = 20.
Qual a interpretação geométrica do resultado acima?
Ora, a derivada da função y = x2 , no ponto de abscissa x = 10 , sendo igual a 20, significa que a tangente trigonométrica da reta tangente à curva y = x2 , no ponto x = 10 , será também igual a 20, conforme teoria vista acima.
Ora, sendo b o ângulo formado por esta reta tangente com o eixo dos x , b será um ângulo tal que tg b = 20. Consultando uma tábua trigonométrica OU através de uma calculadora científica, concluímos que b » 87º 8' 15" .
Então, isto significa que a reta tangente à curva de equação y = x2 , no ponto de abcissa x = 10, forma com o eixo dos x um ângulo igual aproximadamente a b » 87º 8' 15" .
| Agora, calcule como exercício
inicial, usando a definição, a derivada da
função y = 5x no ponto de abscissa x = 1000 . Resposta: 5. |
Paulo Marques - Feira de Santana - BA - 02 de janeiro de 2000.