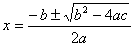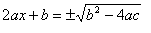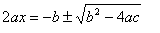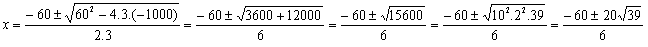-
|
Sobre a fórmula de Bhaskara
|
1
– Introdução
Pretendemos nesta aula, deduzir a fórmula geral de resolução da
equação completa do segundo grau do tipo
ax2
+ bx + c = 0, onde a, b e c são números reais com a ¹
0.
A
conhecida fórmula é dada por:
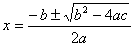
A
fórmula acima é atribuída a Bhaskara –
matemático hindu do século XII (1114 – 1185) –
autor do célebre livro Lilavati, que trata de Álgebra e
Geometria. Lilavati era o nome da sua filha, tendo sido inclusive
o livro escrito na forma de versos.
Existem registros atribuídos ao próprio Bhaskara,
de que a idéia inicial da citada fórmula teria sido desenvolvida no
século X por Sridhara (870 - 960), outro matemático hindu.
Uma biografia (em inglês) deste matemático
hindu pode ser acessada no link SRIDHARA
.
Após visitar o link sugerido, clique em VOLTAR no seu navegador.
É
conveniente ressaltar que a notação (simbologia)
utilizada por Bhaskara para a equação ax2 +
bx + c = 0 não era esta forma compacta usada nos dias de hoje,
pois esta notação literal e intuitiva, somente foi
introduzida no século XVII, por René Descartes, filósofo e matemático francês (1596 - 1650).
2
– Deduzindo a fórmula de Bhaskara
Seja a equação
completa do segundo grau ax2 + bx + c = 0, com a ¹
0.
Isolando
o termo independente c no segundo membro, teremos:
ax2
+ bx = - c
Multiplicando ambos os membros pelo número
4a, vem:
4a(ax2
+ bx) = - 4ac
Desenvolvendo o produto indicado no primeiro
membro, fica:
4a2x2
+ 4abx = - 4ac
Analisando
a igualdade acima, e partindo-se da premissa que uma igualdade não
se altera se adicionarmos quantidades iguais aos dois membros,
poderemos transformar o primeiro membro num quadrado perfeito ,
adicionando b2 a ambos os membros, resultando:
4a2x2
+ 4abx + b2 = - 4ac + b2
Ou
escrevendo de uma forma equivalente:
4a2x2
+ 4abx + b2 = b2 - 4ac
Lembrando da
fórmula conhecida comumente como produto notável:
(m
+ n)2 = m2 + 2mn + n2 , que pode ser
escrita também de modo inverso,
m2 + 2mn + n2
= (m + n)2 , percebemos que o primeiro membro da igualdade
4a2x2
+ 4abx + b2 = b2 - 4ac , pode ser escrito como
(2ax + b)2 . Com efeito, se você desenvolver esta
expressão (usando a fórmula do quadrado de uma soma
vista acima), encontraremos a expressão expandida 4a2x2
+ 4abx + b2 .
Assim,
poderemos escrever a igualdade 4a2x2 + 4abx +
b2 = b2 - 4ac , na forma:
(2ax
+ b)2 = b2 – 4ac
Extraindo a raiz
quadrada de ambos os membros, teremos:
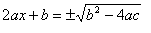
Nota:
Lembre-se que se w2 = z então w = ±
Öz
Passando
o termo b para o segundo membro, fica:
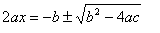
Como o termo a
é diferente de zero, poderemos dividir os dois membros por 2a
¹ 0, resultando
finalmente:
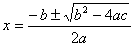
Está
portanto deduzida a famosa Fórmula de Bhaskara para a solução
de equações do segundo grau da forma ax2 +
bx + c = 0,
para a ¹ 0.
Observe que se a = 0, a equação fica apenas bx + c = 0,
que é uma equação do primeiro grau, cuja solução
geral é
x = -c/b, para b diferente de zero (b ¹
0).
Nota:
A
expressão b2 – 4ac é conhecida como
discriminante ou realizante da equação ax2+bx+c=0,
e é representado pela letra grega D
(delta maiúsculo). Assim, D
= b2 – 4ac.
O
termo discriminante possui outros usos na Matemática, porém,
a sua aplicação no caso da equação do
segundo grau pode ser entendida como o fator que discrimina ou
diferencia as soluções da equação, já
que se D > 0, a equação
possuirá duas raízes reais e distintas, se D
= 0, a equação possuirá duas raízes reais
e iguais e se D < 0, a equação
não possuirá raízes reais, embora neste caso, a
equação possui duas raízes não reais, que
são números complexos.
Já a expressão realizante está vinculada
ao fato do discriminante determinar a existência ou não,
de raízes reais da equação ax2 + bx
+c = 0, não sendo entretanto, um termo consagrado pelo uso.
3 –
Um problema clássico
Um
falcão está sobre o topo de uma coluna de dez metros,
em cuja base há um buraco de cobra. Estando a cobra a uma
distância horizontal da coluna igual a três vezes de
altura da coluna, o falcão avançou para a cobra em
linha reta alcançando-a antes que ela chegasse à
sua toca. Se o falcão percorreu o dobro da distância
percorrida pela cobra, qual das alternativas a seguir, representa a
distância aproximada da toca em metros, do ponto onde a cobra
foi alcançada?
A) 11m
B) 15m
C) 17m
D) 19m
E) 25m
Solução:
Observando
a figura abaixo, onde F é a posição
inicial do falcão, C a da cobra, x a distância
percorrida pela cobra (no seu desesperado retorno para a toca!) e 2x
a distância percorrida pelo falcão, poderemos escrever
pelo Teorema de Pitágoras:
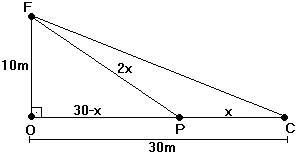
102
+ (30 – x)2 = (2x)2
Desenvolvendo,
vem:
100 + 900 – 60x + x2 = 4x2
1000
– 60x + x2 – 4x2 = 0
1000 –
60x – 3x2 = 0
Ordenando segundo as potências
decrescentes de x, fica:
-3x2
– 60x + 1000 = 0
Multiplicando ambos os membros por (-
1), o que não altera a igualdade, vem:
3x2
+ 60x – 1000 = 0
Temos
uma equação do segundo grau do tipo ax2 + bx
+ c = 0, onde a=3, b=60 e c = -1000.
Aplicando
a fórmula de Bhaskara vista acima, teremos:
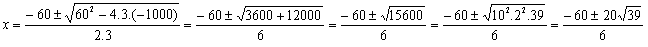
Daí,
tiramos que x = -10 ±
(10/3).Ö39
Como x é
uma distancia e, portanto, um número positivo, a única
raiz que serve ao problema é x = -10 + (10/3).Ö39
. Observe que a outra raiz (x = -10 - (10/3).Ö39)
seria um número negativo e, portanto, como x se refere a uma
distância, este valor negativo não serviria ao problema
proposto.
Portanto,
x @ -10 + (10/3).6,24 @
-10 + 62,4/3 @ -10 + 20,82 @
10,82 m
Notas:
a)
o símbolo @ lê-se como
“ igual aproximadamente a” .
b)
Ö39 @
6,24
c)
6,242 @ 39
Logo, como o problema pede a distância da toca (30
– x), teremos que a resposta será
x = 30 –
10,82 = 19,18m. Das alternativas indicadas, a resposta é a
letra D.
Veja
um outro problema envolvendo a fórmula de Bhaskara: Olhai
os lírios do campo.
Visite
também o arquivo Forma (S,P) de
uma Equação do segundo grau.
Paulo
Marques, Feira de Santana – BA – 08/02/2005 - editado em
04/01/2009.
VOLTAR