Determine as raízes cúbicas do número complexo z = –11 – 2i

Nota: este problema foi enviado para solução, por um ilustre visitante do estado do Piauí.
Realmente, este problema não é tão simples. A solução, na forma de radicais, conforme foi solicitado pelo ilustre visitante do Piauí, repito, não é tão simples assim.  A solução na forma de números decimais, não demoraria muito; bastaria usar uma tabela trigonométrica e a Fórmula de MOIVRE. Mas, achar a solução na forma de radicais, é um pouco difícil. Vamos à solução.

Solução:

Temos um número complexo da forma z = a + bi = –11 – 2i , onde a = – 11 e b = -2; portanto, o seu módulo é igual a


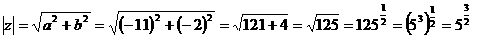
Outro aspecto importante e imprescindível para a solução: a tangente do ângulo formado pelo afixo do Número complexo será dado por  tg θ = -2/-11 = 2/11

A fórmula para o cálculo das raizes cúbicas de um número complexo é dada por



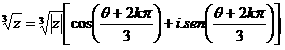
onde, para cada valor de k, obteremos uma das 3 raízes cúbicas existentes.
Assim, por exemplo, para k = 0, obteremos a primeira raiz cúbica de z.

Então, para k = 0, vem para a primeira raiz z₁ :

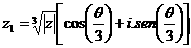
Observe que já conhecemos o valor de |z| = 5^3/2  mas não conhecemos nem cos(θ/3) e nem sen(θ/3).
Conhecemos apenas tgθ = 2/11. Vamos recorrer à fórmula da tangente do arco triplo, a seguir:


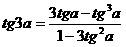
Nota: esta fórmula pode ser obtida facilmente a partir da tangente do arco duplo, fazendo tg3a = tg(2a + a).
Fazendo na equação acima, 3a = θ , obteremos  a = θ/3 e, aí, as coisas começam a clarear.
Substituindo estes valores na equação da tangente do arco triplo vista acima, obteremos:
tgθ = [(3.tg(θ/3) – tg³(θ/3)] / [1 – 3tg²(θ/3)]
Lembrando que tgθ = 2/11 e substituindo, fica:
2/11 = [(3.tg(θ/3) – tg³(θ/3)] / [1 – 3tg²(θ/3)]
Daí, poderemos escrever:
2[1 – 3tg²(θ/3)] = 11[(3.tg(θ/3) – tg³(θ/3)]

Nota: apenas usamos nesta multiplicação, a propriedade fundamental das proporções: o produto dos meios é igual ao produto dos extremos.
Apenas para simplificar a simbologia, façamos a mudança de variável tg(θ/3) = x; a equação fica:
2(1 – 3x²) = 11(3x – x³)
Efetuando as operações indicadas, fica: 2 – 6x² = 33x – 11x³ ou na forma geral: 11x³ – 6x² – 33x + 2 = 0
Trata-se de uma equação polinomial do terceiro grau em x. Poderíamos tentar resolver diretamente esta equação, mas, o caminho seria deveras árduo e tortuoso. Vamos contornar a dificuldade, lembrando que se uma equação polinomial possui raízes inteiras, elas serão necessariamente divisoras do termo independente da equação, que no presente caso é igual a 2. Portanto, se a equação possuir raízes inteiras elas terão que ser ±1 ou ±2, que são os divisores de 2.

Através de mera substituição, concluímos que 2 é raiz pois
11.2³ – 6.2² – 33.2 + 2 = 88 – 24 – 66 + 2 = 88 – 90 + 2 = -2 + 2 = 0.
Ora, se x = 2 então como x = tg(θ/3), vem que tg(θ/3) = 2.
Lembre-se que precisamos conhecer sen(θ/3) e cos(θ/3).
Sabemos da Trigonometria que tgA = senA/cosA  e que sen²A + cos²A = 1. Então, poderemos escrever:
tg(θ/3) = sen(θ/3) / cos(θ/3); substituindo o valor conhecido, fica: 2 = sen(θ/3) / cos(θ/3), de onde tiramos:
sen(θ/3) = 2.cos(θ/3)

Substituindo esta igualdade na relação fundamental da Trigonometria, obteremos:
[2.cos(θ/3)]² + [cos(θ/3)]² = 1 , de onde tiramos: cos(θ/3) = ± √5 / 5.
Agora fica a questão: qual o sinal de cos(θ/3)? Observe o seguinte:  o número complexo dado é z = -11 – 2i, que pode ser representado na forma de par ordenado z = (-11, -2). Ora, o afixo de z está no terceiro quadrante e, por conseguinte o seu argumento θ será tal que 180 < θ < 270 graus e, portanto, dividindo por 3, fica: 60 < θ/3 < 90 graus; logo, θ/3 está no primeiro quadrante e , portanto, tanto o seno como o cosseno serão positivos.
Logo, cos(θ/3) = √5 / 5  e, como já sabemos que neste caso sen(θ/3) = 2.cos(θ/3) , vem: sen(θ/3) = 2√5 / 5.
Ora, como já vimos anteriormente que

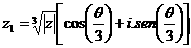
vem, substituindo os valores encontrados anteriormente:


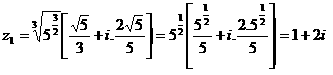
Fiz as contas à parte, num pedaço de papel almaço; faça você também! Vai ser ótimo para o entendimento.
Portanto, a primeira raiz cúbica de z = -11 – 2i é igual a z₁ = 1 + 2i.

Para encontrar a segunda raiz cúbica z₂ façamos k = 1 na fórmula de radiciação de complexos vista no início do texto e reproduzida abaixo:

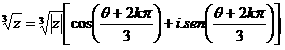
Observe que podemos escrever a igualdade acima para k = 1 , também como:


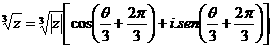
Lembrando que cos(θ/3) = √5 / 5,  sen(θ/3) = 2√5 / 5, cos(2π/3) = -1/2 e sen(2π/3) = √3 / 2, e também lembrando da Trigonometria que:
cos(a+b) = cosa.cosb – sena.senb
sen(a+b) = sena.cosb + senb.cosa
teremos:
cos[(θ/3) + (2π/3)] = cos(θ/3).cos(2π/3) – sen(θ/3).sen(2π/3) = (√5/5).(-1/2) – (2√5/5).(√3/2) = -√5(1 + 2√3)/10
sen[(θ/3) + (2π/3)] = sen(θ/3).cos(2π/3) + sen(2π/3).cos(θ/3) = (2√5/5).(-1/2) + (√5/5).(√3/2) = √5(√3 - 2)/10
Substituindo esses valores vem:
z₂ = -(1+2√3)/2 + i.(√3 - 2)/2

Nota: ajude-se: faça as contas você também!

Para o cálculo da terceira e última raiz cúbica de z, fazendo k = 2 na fórmula de radiciação de complexos, obteremos:
z₃ = (-1+2√3)/2 + i.(-1- √3)
Faça as contas também; vale muito a pena!
Portanto, as três raízes cúbicas do número complexo z = -11 – 2i  são:
z₁ = 1 + 2i
z₂ = -(1+2√3)/2 + i. (√3 - 2)/2
z₃ = (-1+2√3)/2 + i.(-1- √3)
Se você quiser rever o capítulo Números Complexos, clique AQUI.
Para retornar, clique em VOLTAR no seu browser.
Paulo Marques - Feira de Santana - BA , 01 de julho de 2008 - editado em 25 de fevereiro de 2012.

VOLTAR